MATEMÁTICA 9°
SEMANA DEL 03 AL 06 DE NOVIEMBRE
DISTANCIA DE UN PUNTO A UNA RECTA. CONTINUACIÓN
La distancia de un punto a una recta es la longitud del segmento perpendicular a la recta, trazada desde el punto.
Distancia de un punto a una recta



Ejemplo
Calcula la distancia del punto  a la recta
a la recta  de ecuación
de ecuación  .
.




Ejemplo
Calcula la distancia del punto  a la recta
a la recta  de ecuación
de ecuación  .
.

Distancia al origen de coordenadas

Ejemplo
Hallar la distancia al origen de la recta 
.


Ejemplo
Hallar la distancia al origen de la recta 
.

Distancia entre rectas

Para hallar la distancia entre dos en rectas paralelas, se toma un punto cualquiera,  , de una de ellas y calcular su distancia a la otra recta.
, de una de ellas y calcular su distancia a la otra recta.

Ejemplos
1 Hallar la distancia entre  y
y  .
.
Primero comparamos las pendientes para verificar que sean paralelas

Buscamos un punto para alguna de las rectas


Sustituimos en la fórmula de distancia de un punto a una recta

2 Hallar la distancia entre las rectas:






Para hallar la distancia entre dos en rectas paralelas, se toma un punto cualquiera,  , de una de ellas y calcular su distancia a la otra recta.
, de una de ellas y calcular su distancia a la otra recta.

Ejemplos
1 Hallar la distancia entre  y
y  .
.
Primero comparamos las pendientes para verificar que sean paralelas

Buscamos un punto para alguna de las rectas


Sustituimos en la fórmula de distancia de un punto a una recta

2 Hallar la distancia entre las rectas:





SEMANA DEL 26 AL 30 DE OCTUBRE
DISTANCIA DE UN PUNTO A UNA RECTA
La distancia de un punto a una recta es la longitud del segmento perpendicular a la recta, trazada desde el punto.
Distancia de un punto a una recta



Ejemplo
Calcula la distancia del punto  a la recta
a la recta  de ecuación
de ecuación  .
.




Ejemplo
Calcula la distancia del punto  a la recta
a la recta  de ecuación
de ecuación  .
.

Distancia al origen de coordenadas

Ejemplo
Hallar la distancia al origen de la recta 
.


Ejemplo
Hallar la distancia al origen de la recta 
.

Distancia entre rectas

Para hallar la distancia entre dos en rectas paralelas, se toma un punto cualquiera,  , de una de ellas y calcular su distancia a la otra recta.
, de una de ellas y calcular su distancia a la otra recta.

Ejemplos
1 Hallar la distancia entre  y
y  .
.
Primero comparamos las pendientes para verificar que sean paralelas

Buscamos un punto para alguna de las rectas


Sustituimos en la fórmula de distancia de un punto a una recta

2 Hallar la distancia entre las rectas:





SEMANA DEL 19 AL 23 DE OCTUBRE
GEOMETRÍA ANALÍTICA DISTANCIA ENTRE DOS PUNTOS
Distancia entre dos puntos.Dados dos puntos cualesquiera A(x1,y1), B(x2,y2), definimos la distancia entre ellos, d(A,B), como la longitud del segmento que los separa.

Para hallar la distancia entre dos en rectas paralelas, se toma un punto cualquiera,  , de una de ellas y calcular su distancia a la otra recta.
, de una de ellas y calcular su distancia a la otra recta.

Ejemplos
1 Hallar la distancia entre  y
y  .
.
Primero comparamos las pendientes para verificar que sean paralelas

Buscamos un punto para alguna de las rectas


Sustituimos en la fórmula de distancia de un punto a una recta

2 Hallar la distancia entre las rectas:





Historia
Geometría analítica, rama de la Geometría en la que las líneas rectas, las curvas y las figuras geométricas se representan mediante Expresiones algebraicas y numéricas usando un conjunto de ejes y coordenadas. Cualquier punto del Plano se puede localizar con respecto a un par de ejes Perpendiculares dando las distancias del punto a cada uno de los ejes.
Uno los filósofos más notables que contribuyó al desarrollo de las Matemáticas fue [René Descartes]] pues realizó la sistematización de la Geometría Analítica. Fue el primer matemático que intentó clasificar las curvas conforme al tipo de ecuaciones que las producen y contribuyó también a la elaboración de la teoría de las ecuaciones.
Nacido el 31 de marzo de 1596 en La Haye, hoy Descartes, era hijo de un miembro de la baja nobleza y perte- necía a una familia que había dado algu-nos hombres doctos.
En 1649 fue invitado a acudir a Estocolmo para impartir clases de filosofía a la reina Cristina de Suecia. Falleció, en la capital sueca, el 11 de febrero de 1650.
Geometría analítica, rama de la Geometría en la que las líneas rectas, las curvas y las figuras geométricas se representan mediante Expresiones algebraicas y numéricas usando un conjunto de ejes y coordenadas. Cualquier punto del Plano se puede localizar con respecto a un par de ejes Perpendiculares dando las distancias del punto a cada uno de los ejes.
Uno los filósofos más notables que contribuyó al desarrollo de las Matemáticas fue [René Descartes]] pues realizó la sistematización de la Geometría Analítica. Fue el primer matemático que intentó clasificar las curvas conforme al tipo de ecuaciones que las producen y contribuyó también a la elaboración de la teoría de las ecuaciones.
Nacido el 31 de marzo de 1596 en La Haye, hoy Descartes, era hijo de un miembro de la baja nobleza y perte- necía a una familia que había dado algu-nos hombres doctos.
En 1649 fue invitado a acudir a Estocolmo para impartir clases de filosofía a la reina Cristina de Suecia. Falleció, en la capital sueca, el 11 de febrero de 1650.
Distancia entre dos puntos
El Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.
Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1).
Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. (y1 - y2)
Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
El Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.
Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1).
Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. (y1 - y2)
Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Demostración
SEMANA DEL 13 AL 16 DE OCTUBRERECTAS PARALELAS Y RECTAS PERPENDICULARES
Las rectas paralelas son dos o más rectas en un plano que nunca se intersectan. Hay muchos ejemplos de rectas paralelas como los lados opuestos del marco rectangular de una pintura y los estantes de un librero.
Las rectas perpendiculares son dos o más rectas que se intersectan formando un ángulo de 90 grados, como las dos rectas dibujadas en la gráfica. Los ángulos de 90 grados también se llaman ángulos rectos.
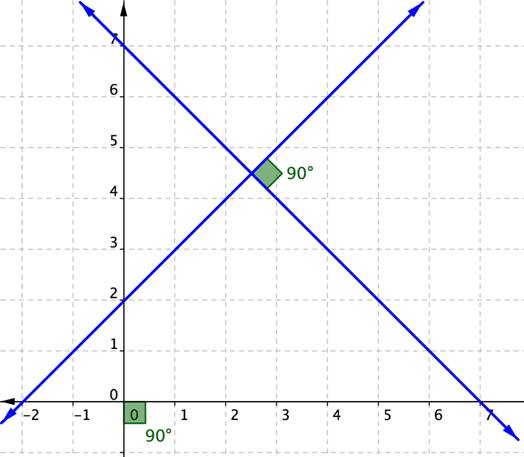
Las rectas perpendiculares también están en todos lados, no sólo en una gráfica en papel sino en el mundo real, desde el patrón de cruce en las calles a la intersección de las líneas coloreadas de una camisa a cuadros.
Explora las rectas en el diagrama interactivo siguiente.
o Haz clic y arrastra el punto en el deslizante “Ecuación” para elegir uno de 5 ejemplos de ecuaciones. La ecuación se grafica en azul.
o Luego, haz clic y arrastra el punto en la recta roja para hacerla paralela o perpendicular a la recta azul. (Asegúrate de mover lentamente el cursor.) ¡Cuando las rectas son paralelas o perpendiculares, aparecerá un texto para avisarte que ya le atinaste!
o Observa las pendientes de las dos rectas paralelas. ¿Qué es lo que notas? Observa las pendientes de las rectas perpendiculares. ¿Qué es lo que notas?
o Escoge otra ecuación e inténtalo de nuevo.
o Conforme intentas con otras ecuaciones, observa la relación entre las pendientes de rectas paralelas, y las pendientes de rectas perpendiculares. Al intentar con la última ecuación, ¿puedes predecir cuáles serán las pendientes de las rectas paralelas y perpendiculares?
Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)
De la primera exploración, habrás notado lo siguiente.
Rectas Paralelas
Dos rectas no verticales en un plano son paralelas si tienen:
o la misma pendiente
o distintas intersecciones en y
Cualquier par de rectas verticales en un plano son paralelas.
Ejemplo
Problema
Encontrar la pendiente de una recta que es paralela a la recta y = −3x + 4.
La recta dada se escribe como y = mx + b, con m = −3 y b = 4. La pendiente es −3.
Identifica la pendiente de la recta dada.
Respuesta
La pendiente de la recta paralela es −3.
Una recta paralela a la recta dada tiene la misma pendiente.
Ejemplo
Problema
Determina si las rectas y = 6x + 5 y y = 6x – 1 son paralelas.
La recta dada se escribe como y = mx + b con m = 6 para la primera recta y m = 6 para la segunda recta. La pendiente de ambas rectas es 6.
Identifica la pendiente de la recta dada.
La primera recta tiene una intersección en <i>y</i> en (0, 5), y la segunda recta tiene una intersección en <i>y</i> en (0, −1). No son la misma recta.
Observa b, el valor de y de la intersección en <i>y</i>, para ver si las rectas son la misma, en cuyo caso no decimos que son paralelas.
Respuesta
Las rectas son paralelas.
Las pendientes de las rectas son las mismas y tienen diferentes intersecciones en y, entonces no son la misma recta y son paralelas.
Rectas Perpendiculares
Dos rectas no verticales son perpendiculares si la pendiente de una es el recíproco negativo de la pendiente de la otra. Si la pendiente de la primera ecuación es 4, entonces la pendiente de la segunda ecuación será  porque las rectas son perpendiculares.
porque las rectas son perpendiculares.
También puedes probar las pendientes para ver si las rectas son perpendiculares multiplicando las dos pendientes. Si son perpendiculares, el producto de las pendientes será −1. Por ejemplo,  .
.
Ejemplo
Problema
Encontrar la pendiente de la recta perpendicular a la recta y = 2x – 6.
La recta dada se escribe como y = mx + b, con m = 2 y b = -6. La pendiente es 2.
Identifica la pendiente de la recta dada.
Respuesta
La pendiente de la recta perpendicular es  .
.
Para encontrar la pendiente de la recta perpendicular, encuentra el recíproco,  , y luego encuentra el opuesto del recíproco
, y luego encuentra el opuesto del recíproco  .
.
Observa que el producto  , lo que significa que las pendientes son perpendiculares.
, lo que significa que las pendientes son perpendiculares.
En el caso donde una de las rectas es vertical, la pendiente de esa recta no está definida y no es posible calcular el producto de un número indefinido. Cuando una recta es vertical, la recta perpendicular a ella será horizontal, teniendo una pendiente de cero (m = 0).
Ejemplo
Problema
Determinar si las rectas y = −8x + 5 y  son paralelas, perpendiculares, o ninguna.
son paralelas, perpendiculares, o ninguna.
Las rectas dadas están escritas en la forma y = mx + b, con m = −8 para la primera recta y m =  para la segunda recta.
para la segunda recta.
Identifica las pendientes de las rectas dadas.
−8 ≠  , entonces las rectas no so paralelas.
, entonces las rectas no so paralelas.
El recíproco opuesto de −8 es  , entonces las rectas son perpendiculares.
, entonces las rectas son perpendiculares.
Determina si las pendientes son la misma o si son recíprocas opuestas.
Respuesta
Las rectas son perpendiculares.
Las pendientes de las rectas son recíprocas opuestas, por lo que las rectas son perpendiculares.
¿Cuáles de las siguientes rectas son perpendiculares a la recta  ?
?




A)  y
y 
B)  y
y 
C) 
D) Todas las rectas son perpendiculares.
Las relaciones entre pendientes de rectas paralelas y perpendiculares pueden usarse para escribir ecuaciones de rectas paralelas y perpendiculares.
Empecemos con un ejemplo de rectas paralelas.
Ejemplo
Problema
Escribir la ecuación de una recta que sea paralela a la recta x – y = 5 y pase por el punto (−2, 1).
x – y = 5
−y = −x + 5
y = x – 5
Reescribe, si es necesario, la recta que quieres que sea paralela de la forma
y = mx + b.
En la ecuación anterior, m = 1 y b = −5.
Como m = 1, la pendiente es 1.
Identifica la pendiente de la recta dada.
La pendiente de la recta paralela es 1.
Para encontrar la pendiente de una recta paralela, usa la misma pendiente.
y = mx + b
1 = 1(−2) + b
Usa el método para escribir una ecuación a partir de la pendiente y un punto en la recta. Sustituye 1 por m, y el punto (−2, 1) por x y y.
1 = −2 + b
3 = b
Resuelve b.
Respuesta
y = x + 3
Escribe la ecuación usando la nueva pendiente para m y la b que acabas de encontrar.
Cuando trabajas con rectas perpendiculares, normalmente tendrás una de las rectas y un punto adicional.
Ejemplo
Problema
Escribir la ecuación de una recta que contenga el punto(1, 5) y sea perpendicular a la recta y = 2x – 6.
La recta dada se escribe en la forma y = mx + b, como m = 2 y b = -6. La pendiente es 2.
Identifica la pendiente de la recta con la que tu recta debe ser perpendicular.
La pendiente de la recta paralela es  .
.
Para encontrar la pendiente de una recta perpendicular, encuentra el recíproco,  , y luego su opuesto,
, y luego su opuesto,  .
.

Usando el método de escribir una ecuación a partir de su pendiente y un punto en la recta. Sustituye  por m, y el punto (1, 5) por x y y.
por m, y el punto (1, 5) por x y y.


Resuelve b.
Respuesta

Escribe la ecuación usando la nueva pendiente para m y la b que acabas de encontrar.
¿Cuál de la siguientes es la ecuación de una recta paralela a y = −2x – 14 y pasa por el punto (−3, 1)?
A) y = −2x + 1
B) 
C) 
D) y = −2x – 5
Ejemplo
Problema
Escribir la ecuación de una recta que sea paralela a y = 4.
y = 4
y = 0x + 4
Reescribe, si es necesario, la recta en la forma
y = mx + b.
Podrás haber notado sin hacerlo que y = 4 es una recta horizontal 4 unidades sobre el eje-x. Porque es horizontal, y sabes que la pendiente es cero.
En la ecuación anterior, m = 0 y b = 4.
Como m = 0, la pendiente es 0. Esta es una recta horizontal.
Identifica la pendiente de la recta dada.
La pendiente de la recta paralela también es 0.
Para encontrar la pendiente de una recta paralela, usa la misma pendiente.
y = 10
Como la recta paralela será una recta horizontal, su forma es
y = una constante.
Escoge una constante para crear la recta paralela.
Respuesta
y = 10
Esta recta es paralela a y = 4 e intersecta el eje-y en (0, 10).
Sumario
Cuando rectas en un plano so paralelas (es decir, nunca se cruzan), tienen la misma pendiente. Cuando rectas son perpendiculares (es decir, se cruzan formando un ángulo de 90°), sus pendientes son recíprocas opuestas una de la otra. El producto de sus pendientes siempre será -1, excepto en el caso donde una de las rectas es vertical, porque su pendiente no está definida. Puedes usar estas relaciones para encontrar la ecuación de una recta que pase por un punto en particular y que sea paralela o perpendicular a otra recta.
La ecuación de una recta es

El coeficiente es la pendiente y es la ordenada en el origen.
El valor de la pendiente, , es la causa de un mayor o menor crecimiento.
Las rectas paralelas son dos o más rectas en un plano que nunca se intersectan. Hay muchos ejemplos de rectas paralelas como los lados opuestos del marco rectangular de una pintura y los estantes de un librero.
Las rectas perpendiculares son dos o más rectas que se intersectan formando un ángulo de 90 grados, como las dos rectas dibujadas en la gráfica. Los ángulos de 90 grados también se llaman ángulos rectos.

Las rectas perpendiculares también están en todos lados, no sólo en una gráfica en papel sino en el mundo real, desde el patrón de cruce en las calles a la intersección de las líneas coloreadas de una camisa a cuadros.
Explora las rectas en el diagrama interactivo siguiente.
o Haz clic y arrastra el punto en el deslizante “Ecuación” para elegir uno de 5 ejemplos de ecuaciones. La ecuación se grafica en azul.
o Luego, haz clic y arrastra el punto en la recta roja para hacerla paralela o perpendicular a la recta azul. (Asegúrate de mover lentamente el cursor.) ¡Cuando las rectas son paralelas o perpendiculares, aparecerá un texto para avisarte que ya le atinaste!
o Observa las pendientes de las dos rectas paralelas. ¿Qué es lo que notas? Observa las pendientes de las rectas perpendiculares. ¿Qué es lo que notas?
o Escoge otra ecuación e inténtalo de nuevo.
o Conforme intentas con otras ecuaciones, observa la relación entre las pendientes de rectas paralelas, y las pendientes de rectas perpendiculares. Al intentar con la última ecuación, ¿puedes predecir cuáles serán las pendientes de las rectas paralelas y perpendiculares?
Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)
De la primera exploración, habrás notado lo siguiente.
Rectas Paralelas
Dos rectas no verticales en un plano son paralelas si tienen: o la misma pendiente o distintas intersecciones en y
Cualquier par de rectas verticales en un plano son paralelas. |
Ejemplo | ||
Problema | Encontrar la pendiente de una recta que es paralela a la recta y = −3x + 4. | |
| La recta dada se escribe como y = mx + b, con m = −3 y b = 4. La pendiente es −3. | Identifica la pendiente de la recta dada. |
Respuesta | La pendiente de la recta paralela es −3. | Una recta paralela a la recta dada tiene la misma pendiente. |
Ejemplo | |||
Problema | Determina si las rectas y = 6x + 5 y y = 6x – 1 son paralelas. | ||
| La recta dada se escribe como y = mx + b con m = 6 para la primera recta y m = 6 para la segunda recta. La pendiente de ambas rectas es 6. | Identifica la pendiente de la recta dada. | |
| La primera recta tiene una intersección en <i>y</i> en (0, 5), y la segunda recta tiene una intersección en <i>y</i> en (0, −1). No son la misma recta. | Observa b, el valor de y de la intersección en <i>y</i>, para ver si las rectas son la misma, en cuyo caso no decimos que son paralelas. | |
Respuesta | Las rectas son paralelas. | Las pendientes de las rectas son las mismas y tienen diferentes intersecciones en y, entonces no son la misma recta y son paralelas. | |
Rectas Perpendiculares Dos rectas no verticales son perpendiculares si la pendiente de una es el recíproco negativo de la pendiente de la otra. Si la pendiente de la primera ecuación es 4, entonces la pendiente de la segunda ecuación será |
También puedes probar las pendientes para ver si las rectas son perpendiculares multiplicando las dos pendientes. Si son perpendiculares, el producto de las pendientes será −1. Por ejemplo, ![]() .
.
Ejemplo | ||
Problema | Encontrar la pendiente de la recta perpendicular a la recta y = 2x – 6. | |
| La recta dada se escribe como y = mx + b, con m = 2 y b = -6. La pendiente es 2. | Identifica la pendiente de la recta dada. |
Respuesta |
La pendiente de la recta perpendicular es | Para encontrar la pendiente de la recta perpendicular, encuentra el recíproco, |
Observa que el producto ![]() , lo que significa que las pendientes son perpendiculares.
, lo que significa que las pendientes son perpendiculares.
En el caso donde una de las rectas es vertical, la pendiente de esa recta no está definida y no es posible calcular el producto de un número indefinido. Cuando una recta es vertical, la recta perpendicular a ella será horizontal, teniendo una pendiente de cero (m = 0).
Ejemplo | ||
Problema | Determinar si las rectas y = −8x + 5 y | |
| Las rectas dadas están escritas en la forma y = mx + b, con m = −8 para la primera recta y m = | Identifica las pendientes de las rectas dadas. |
| −8 ≠ El recíproco opuesto de −8 es | Determina si las pendientes son la misma o si son recíprocas opuestas. |
Respuesta | Las rectas son perpendiculares. | Las pendientes de las rectas son recíprocas opuestas, por lo que las rectas son perpendiculares. |
¿Cuáles de las siguientes rectas son perpendiculares a la recta
A)
B)
C)
D) Todas las rectas son perpendiculares.
|
Las relaciones entre pendientes de rectas paralelas y perpendiculares pueden usarse para escribir ecuaciones de rectas paralelas y perpendiculares.
Empecemos con un ejemplo de rectas paralelas.
Ejemplo | ||
Problema | Escribir la ecuación de una recta que sea paralela a la recta x – y = 5 y pase por el punto (−2, 1). | |
| x – y = 5 −y = −x + 5 y = x – 5 | Reescribe, si es necesario, la recta que quieres que sea paralela de la forma y = mx + b. |
| En la ecuación anterior, m = 1 y b = −5. Como m = 1, la pendiente es 1. | Identifica la pendiente de la recta dada. |
| La pendiente de la recta paralela es 1. | Para encontrar la pendiente de una recta paralela, usa la misma pendiente. |
| y = mx + b 1 = 1(−2) + b | Usa el método para escribir una ecuación a partir de la pendiente y un punto en la recta. Sustituye 1 por m, y el punto (−2, 1) por x y y. |
| 1 = −2 + b 3 = b | Resuelve b. |
Respuesta | y = x + 3 | Escribe la ecuación usando la nueva pendiente para m y la b que acabas de encontrar. |
Cuando trabajas con rectas perpendiculares, normalmente tendrás una de las rectas y un punto adicional.
Ejemplo | ||
Problema | Escribir la ecuación de una recta que contenga el punto(1, 5) y sea perpendicular a la recta y = 2x – 6. | |
| La recta dada se escribe en la forma y = mx + b, como m = 2 y b = -6. La pendiente es 2. | Identifica la pendiente de la recta con la que tu recta debe ser perpendicular. |
| La pendiente de la recta paralela es | Para encontrar la pendiente de una recta perpendicular, encuentra el recíproco, |
|
| Usando el método de escribir una ecuación a partir de su pendiente y un punto en la recta. Sustituye |
|
| Resuelve b. |
Respuesta |
| Escribe la ecuación usando la nueva pendiente para m y la b que acabas de encontrar. |
¿Cuál de la siguientes es la ecuación de una recta paralela a y = −2x – 14 y pasa por el punto (−3, 1)?
A) y = −2x + 1
B)
C)
D) y = −2x – 5
|
Ejemplo | ||
Problema | Escribir la ecuación de una recta que sea paralela a y = 4. | |
| y = 4 y = 0x + 4
| Reescribe, si es necesario, la recta en la forma y = mx + b. Podrás haber notado sin hacerlo que y = 4 es una recta horizontal 4 unidades sobre el eje-x. Porque es horizontal, y sabes que la pendiente es cero. |
| En la ecuación anterior, m = 0 y b = 4. Como m = 0, la pendiente es 0. Esta es una recta horizontal. | Identifica la pendiente de la recta dada. |
| La pendiente de la recta paralela también es 0. | Para encontrar la pendiente de una recta paralela, usa la misma pendiente. |
|
y = 10 | Como la recta paralela será una recta horizontal, su forma es y = una constante. Escoge una constante para crear la recta paralela. |
Respuesta | y = 10 | Esta recta es paralela a y = 4 e intersecta el eje-y en (0, 10). |
Sumario
Cuando rectas en un plano so paralelas (es decir, nunca se cruzan), tienen la misma pendiente. Cuando rectas son perpendiculares (es decir, se cruzan formando un ángulo de 90°), sus pendientes son recíprocas opuestas una de la otra. El producto de sus pendientes siempre será -1, excepto en el caso donde una de las rectas es vertical, porque su pendiente no está definida. Puedes usar estas relaciones para encontrar la ecuación de una recta que pase por un punto en particular y que sea paralela o perpendicular a otra recta.
La ecuación de una recta es

El coeficiente es la pendiente y es la ordenada en el origen.
El valor de la pendiente, , es la causa de un mayor o menor crecimiento.
Ejemplo 1
La recta crece más rápido que porque tiene una pendiente mayor:
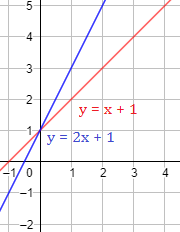
El valor de la ordenada en el origen, , es la segunda coordenada del punto de corte de la recta con el eje Y.
La recta crece más rápido que porque tiene una pendiente mayor:

El valor de la ordenada en el origen, , es la segunda coordenada del punto de corte de la recta con el eje Y.
Ejemplo 2
La recta corta al eje Y en y la recta lo hace en el punto :
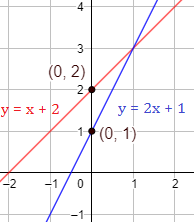
La recta corta al eje Y en y la recta lo hace en el punto :

2. Paralelas
Dos rectas son paralelas cuando no se cortan. Esto ocurre cuando las rectas tienen la misma pendiente.
Dos rectas son paralelas cuando no se cortan. Esto ocurre cuando las rectas tienen la misma pendiente.
Ejemplo 3
Las rectas e son paralelas. Observad que tienen la misma pendiente, :
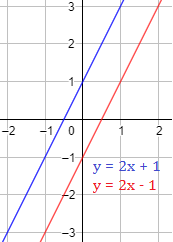
Las rectas e son paralelas. Observad que tienen la misma pendiente, :

3. Perpendiculares
Dos rectas son perpendiculares cuando se cortan formando un ángulo recto (ángulo de 45°).
Esto ocurre cuando la pendiente de una de las rectas es el opuesto del inverso de la otra. Es decir, si la pendiente de una de las rectas es , la otra debe ser .
Dos rectas son perpendiculares cuando se cortan formando un ángulo recto (ángulo de 45°).
Esto ocurre cuando la pendiente de una de las rectas es el opuesto del inverso de la otra. Es decir, si la pendiente de una de las rectas es , la otra debe ser .
Ejemplo 4
Las rectas e son perpendiculares:
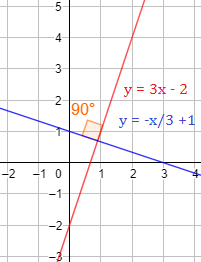
Las rectas e son perpendiculares:

4. Problemas resueltos
Problema 1
Determinar si las siguientes rectas son o no paralelas o perpendiculares:
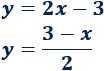
La pendiente de la recta es .
Podemos reescribir la segunda recta:
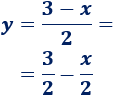
De este modo, vemos mejor que la pendiente es .
Las rectas son perpendiculares porque .
Representación:
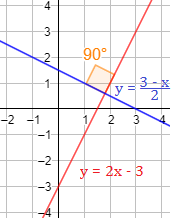
Problema 2
Determinar si las siguientes rectas son o no paralelas o perpendiculares:
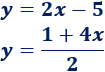
SoluciónLa pendiente de la recta es .
Observad que podemos escribir la segunda recta de otro modo:
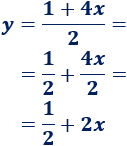
De este modo, se observa que la pendiente de esta recta también es . Por tanto, son rectas paralelas.
Representación:
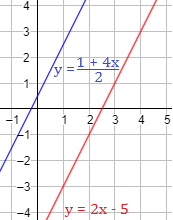
Determinar si las siguientes rectas son o no paralelas o perpendiculares:
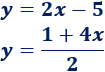
La pendiente de la recta es .
Observad que podemos escribir la segunda recta de otro modo:
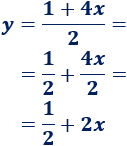
De este modo, se observa que la pendiente de esta recta también es . Por tanto, son rectas paralelas.
Representación:

Problema 3
Hallar la recta paralela a la recta y que pasa por el punto .
SoluciónLa ecuación de una recta es

Como la recta que buscamos debe ser paralela a la recta , su pendiente debe ser la misma. Por tanto, .
Podemos calcular sustituyendo las coordenadas del punto en la ecuación de la recta:
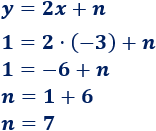
Por tanto, la recta que buscamos es

Representación:
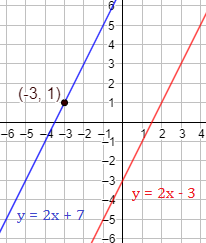
Hallar la recta paralela a la recta y que pasa por el punto .
La ecuación de una recta es

Como la recta que buscamos debe ser paralela a la recta , su pendiente debe ser la misma. Por tanto, .
Podemos calcular sustituyendo las coordenadas del punto en la ecuación de la recta:
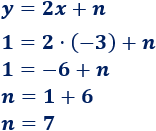
Por tanto, la recta que buscamos es

Representación:

Problema 4
Hallar la recta perpendicular a la recta y que pasa por el punto .
SoluciónLa ecuación de una recta es

Como la recta debe ser perpendicular a , su pendiente debe ser .
Calculamos sustituyendo las coordenadas del punto en la ecuación:
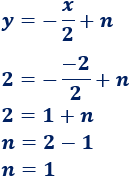
Por tanto, es la recta
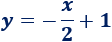
Representación:
Hallar la recta perpendicular a la recta y que pasa por el punto .
La ecuación de una recta es

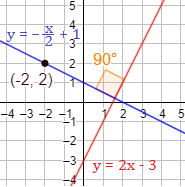
Como la recta debe ser perpendicular a , su pendiente debe ser .
Calculamos sustituyendo las coordenadas del punto en la ecuación:
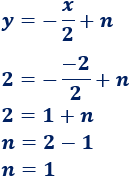
Por tanto, es la recta
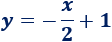
Representación:

Problema 5
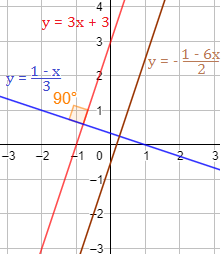
Determinar si las siguientes rectas son perpendiculares a la recta :
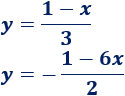
SoluciónReescribimos la primera ecuación:
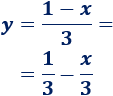
Su pendiente es . Esta recta es perpendicular a .
Reescribimos la segunda ecuación:
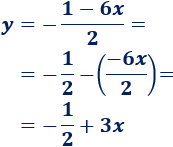
Su pendiente es . Esta recta es paralela a .
Representación:
SEMANA 28 DE SEPTIEMBRE AL 02 DE OCTUBRE
TRANSFORMAR LA ECUACIÓN GENERAL DE LA RECTA EN ECUACIÓN EXPLÍCITA
Determinar si las siguientes rectas son perpendiculares a la recta :
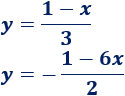
Reescribimos la primera ecuación:
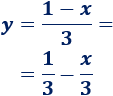
Su pendiente es . Esta recta es perpendicular a .
Reescribimos la segunda ecuación:
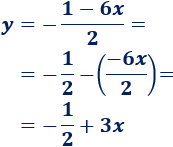
Su pendiente es . Esta recta es paralela a .
Representación:

Ecuación explicita de la recta
¿Cuál es la ecuación de la recta en forma explícita?
La ecuación explícita de la recta es de la forma

donde  es la pendiente y
es la pendiente y  la ordenada a origen.
la ordenada a origen.
La ecuación explícita de la recta es de la forma

donde  es la pendiente y
es la pendiente y  la ordenada a origen.
la ordenada a origen.
Forma explícita de la recta a partir de la ecuación general
Si en la ecuación general de la recta

despejamos  , se obtiene la ecuación explícita de la recta
, se obtiene la ecuación explícita de la recta

Hacemos

y obtenemos

Si en la ecuación general de la recta

despejamos  , se obtiene la ecuación explícita de la recta
, se obtiene la ecuación explícita de la recta

Hacemos

y obtenemos

Ejemplo de ejercicios con la forma explícita de la recta
Hallar la ecuación en forma explícita de la recta que pasa por  y tiene como pendiente
y tiene como pendiente  .
.
1Sabemos que la pendiente es igual al cociente  , por lo que tenemos
, por lo que tenemos

2Sustituimos el punto  en la ecuación general de la recta, el valor de
en la ecuación general de la recta, el valor de  en términos de
en términos de  y obtenemos
y obtenemos

3Despejamos  en términos de
en términos de  y obtenemos
y obtenemos

4Sustituimos los valores de  y
y  en la ecuación general de la recta y factorizamos el término común
en la ecuación general de la recta y factorizamos el término común

5Como  , dividimos ambos términos de la ecuación entre
, dividimos ambos términos de la ecuación entre 

6Despejamos  y obtenemos la ecuación explícita de la recta
y obtenemos la ecuación explícita de la recta

Hallar la ecuación en forma explícita de la recta que pasa por  y tiene como pendiente
y tiene como pendiente  .
.
1Sabemos que la pendiente es igual al cociente  , por lo que tenemos
, por lo que tenemos

2Sustituimos el punto  en la ecuación general de la recta, el valor de
en la ecuación general de la recta, el valor de  en términos de
en términos de  y obtenemos
y obtenemos

3Despejamos  en términos de
en términos de  y obtenemos
y obtenemos

4Sustituimos los valores de  y
y  en la ecuación general de la recta y factorizamos el término común
en la ecuación general de la recta y factorizamos el término común

5Como  , dividimos ambos términos de la ecuación entre
, dividimos ambos términos de la ecuación entre 

6Despejamos  y obtenemos la ecuación explícita de la recta
y obtenemos la ecuación explícita de la recta

Forma explícita de la recta a partir de la ecuación punto-pendiente
Si en la ecuación punto-pendiente de la recta

despejamos  , se obtiene la ecuación explícita de la recta
, se obtiene la ecuación explícita de la recta

Hacemos

y obtenemos

Ejemplo:
Hallar la ecuación en forma explícita de la recta que pasa por  y tiene como pendiente
y tiene como pendiente  .
.
1Sustituimos el punto y la pendiente en la ecuación punto-pendiente de la recta y obtenemos

2Despejamos  y obtenemos la ecuación explícita de la recta
y obtenemos la ecuación explícita de la recta

SEMANA 21 AL 25 DE SEPTIEMBREECUACIONES DE UNA RECTA
REPASO
Si en la ecuación punto-pendiente de la recta

despejamos  , se obtiene la ecuación explícita de la recta
, se obtiene la ecuación explícita de la recta

Hacemos

y obtenemos

Ejemplo:
Hallar la ecuación en forma explícita de la recta que pasa por  y tiene como pendiente
y tiene como pendiente  .
.
1Sustituimos el punto y la pendiente en la ecuación punto-pendiente de la recta y obtenemos

2Despejamos  y obtenemos la ecuación explícita de la recta
y obtenemos la ecuación explícita de la recta

Ecuación de la recta
(Segundo medio)
Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano .
La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).
La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).

La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.
El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta .
Para comprender este proceder es como si la misma línea solo se cambia de ropa para que sepan de su existencia pero expresada en términos matemáticos (como una ecuación).
Es en este contexto que la Geometría analítica nos enseña que una recta es la representación gráfica de una expresión algebraica (función) o ecuación lineal de primer grado .
Esta ecuación de la recta varía su formulación de acuerdo con los datos que se conozcan de la línea recta que se quiere representar algebraicamente. Dicho en otras palabras, hay varias formas de representar la ecuación de la recta.
1.– Ecuación general de la recta
Esta es una de las formas de representar la ecuación de la recta.
De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano) , con abscisas (x) y ordenadas (y) .
Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano.
Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación
(Segundo medio)
Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano .
La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).
La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).
 |
La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.
El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta .
Para comprender este proceder es como si la misma línea solo se cambia de ropa para que sepan de su existencia pero expresada en términos matemáticos (como una ecuación).
Es en este contexto que la Geometría analítica nos enseña que una recta es la representación gráfica de una expresión algebraica (función) o ecuación lineal de primer grado .
Esta ecuación de la recta varía su formulación de acuerdo con los datos que se conozcan de la línea recta que se quiere representar algebraicamente. Dicho en otras palabras, hay varias formas de representar la ecuación de la recta.
1.– Ecuación general de la recta
Esta es una de las formas de representar la ecuación de la recta.
De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano) , con abscisas (x) y ordenadas (y) .
| Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano. |
Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación
Ax + By + C = 0
Que también puede escribirse como
Que también puede escribirse como
ax + by + c = 0
y que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente:
Teorema
La ecuación general de primer grado Ax + By + C = 0 , donde A, B, C pertenecen a los números reales ( 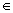
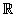 ); y en que A y B no son simultáneamente nulos, representa una línea recta.
); y en que A y B no son simultáneamente nulos, representa una línea recta.
2.– Ecuación principal de la recta
Esta es otra de las formas de representar la ecuación de la recta.
Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:
Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa (horizontal) e y el valor de la ordenada (vertical).
y que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente:
Teorema La ecuación general de primer grado Ax + By + C = 0 , donde A, B, C pertenecen a los números reales ( |
2.– Ecuación principal de la recta
Esta es otra de las formas de representar la ecuación de la recta.
Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:
Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa (horizontal) e y el valor de la ordenada (vertical).
(x, y) = (Abscisa , Ordenada)
Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.
Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.
Ejemplo: El punto ( 7, 2 ) (el 7 en la abscisa x y el 2 en la ordenada y ) satisface la ecuación y = x – 5 , ya que al reemplazar queda
2 = 7 – 5 lo que resulta verdadero.
Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce , que se obtiene con la fórmula
Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.
Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.
Ejemplo: El punto ( 7, 2 ) (el 7 en la abscisa x y el 2 en la ordenada y ) satisface la ecuación y = x – 5 , ya que al reemplazar queda
2 = 7 – 5 lo que resulta verdadero.
Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce , que se obtiene con la fórmula
y = mx + n
que considera las siguientes variables: un punto ( x, y ), la pendiente ( m ) y el punto de intercepción en la ordenada ( n ), y es conocida como ecuación principal de la recta (conocida también como forma simplificada, como veremos luego).
Al representar la ecuación de la recta en su forma principal vemos que aparecieron dos nuevas variables: la m y la n , esto agrega a nuestra ecuación de la recta dos nuevos elementos que deben considerase al analizar o representar una recta: la pendiente (m) y el punto de intercepción (n) (también llamado intercepto ) en el eje de las ordenadas (y) .
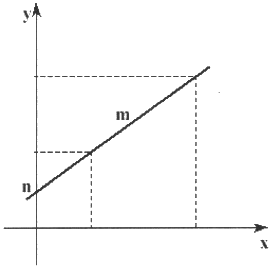
Respecto a esto, en el gráfico de arriba, m representa la pendiente de la recta y permite obtener su grado de inclinación (en relación a la horizontal o abscisa), y n es el coeficiente de posición, el número que señala el punto donde la recta interceptará al eje de las ordenadas (y).
que considera las siguientes variables: un punto ( x, y ), la pendiente ( m ) y el punto de intercepción en la ordenada ( n ), y es conocida como ecuación principal de la recta (conocida también como forma simplificada, como veremos luego).
Al representar la ecuación de la recta en su forma principal vemos que aparecieron dos nuevas variables: la m y la n , esto agrega a nuestra ecuación de la recta dos nuevos elementos que deben considerase al analizar o representar una recta: la pendiente (m) y el punto de intercepción (n) (también llamado intercepto ) en el eje de las ordenadas (y) .
 |
Respecto a esto, en el gráfico de arriba, m representa la pendiente de la recta y permite obtener su grado de inclinación (en relación a la horizontal o abscisa), y n es el coeficiente de posición, el número que señala el punto donde la recta interceptará al eje de las ordenadas (y).
Forma simplificada de la ecuación de la recta
Si se conoce la pendiente m , y el punto donde la recta corta al eje de ordenadas es ( 0, b ) (corresponde a n en la fórmula principal ya vista), podemos deducir, partiendo de la ecuación de la recta de la forma
Forma simplificada de la ecuación de la recta
Si se conoce la pendiente m , y el punto donde la recta corta al eje de ordenadas es ( 0, b ) (corresponde a n en la fórmula principal ya vista), podemos deducir, partiendo de la ecuación de la recta de la forma
y − y 1 = m(x − x 1 )
y – b = m(x – 0)
y – b = mx
y = mx + b
Esta es una segunda forma de la ecuación principal de la recta (se la llama también forma explícita de la ecuación ) y se utiliza cuando se conocen la pendiente y la ordenada al origen (o intercepto), que llamaremos b ( no olvidemos que corresponde a la n en la primera forma de la ecuación principal). También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo cual indica que interceptará al eje y en el punto (0, 7) .
Conocida la fórmula de la ecuación principal (simplificada o explícita, como quieran llamarla) de la recta es posible obtener la ecuación de cualquier recta siempre que se nos den al menos dos variables de ella: puede ser la pendiente, puede ser un punto o puede ser el intercepto.
Esta es una segunda forma de la ecuación principal de la recta (se la llama también forma explícita de la ecuación ) y se utiliza cuando se conocen la pendiente y la ordenada al origen (o intercepto), que llamaremos b ( no olvidemos que corresponde a la n en la primera forma de la ecuación principal). También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo cual indica que interceptará al eje y en el punto (0, 7) .
Conocida la fórmula de la ecuación principal (simplificada o explícita, como quieran llamarla) de la recta es posible obtener la ecuación de cualquier recta siempre que se nos den al menos dos variables de ella: puede ser la pendiente, puede ser un punto o puede ser el intercepto.
SEMANA 07 AL 11 DE SEPTIEMBREECUACIONES DE UNA RECTA
Ecuación de la recta
(Segundo medio)
Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano .
La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).
La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).

La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.
El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta .
Para comprender este proceder es como si la misma línea solo se cambia de ropa para que sepan de su existencia pero expresada en términos matemáticos (como una ecuación).
Es en este contexto que la Geometría analítica nos enseña que una recta es la representación gráfica de una expresión algebraica (función) o ecuación lineal de primer grado .
Esta ecuación de la recta varía su formulación de acuerdo con los datos que se conozcan de la línea recta que se quiere representar algebraicamente. Dicho en otras palabras, hay varias formas de representar la ecuación de la recta.
1.– Ecuación general de la recta
Esta es una de las formas de representar la ecuación de la recta.
De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano) , con abscisas (x) y ordenadas (y) .
Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano.
Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación
(Segundo medio)
Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano .
La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).
La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).
 |
La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.
El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta .
Para comprender este proceder es como si la misma línea solo se cambia de ropa para que sepan de su existencia pero expresada en términos matemáticos (como una ecuación).
Es en este contexto que la Geometría analítica nos enseña que una recta es la representación gráfica de una expresión algebraica (función) o ecuación lineal de primer grado .
Esta ecuación de la recta varía su formulación de acuerdo con los datos que se conozcan de la línea recta que se quiere representar algebraicamente. Dicho en otras palabras, hay varias formas de representar la ecuación de la recta.
1.– Ecuación general de la recta
Esta es una de las formas de representar la ecuación de la recta.
De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano) , con abscisas (x) y ordenadas (y) .
| Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano. |
Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación
Ax + By + C = 0
Que también puede escribirse como
Que también puede escribirse como
ax + by + c = 0
y que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente:
Teorema
La ecuación general de primer grado Ax + By + C = 0 , donde A, B, C pertenecen a los números reales ( 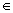
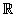 ); y en que A y B no son simultáneamente nulos, representa una línea recta.
); y en que A y B no son simultáneamente nulos, representa una línea recta.
2.– Ecuación principal de la recta
Esta es otra de las formas de representar la ecuación de la recta.
Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:
Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa (horizontal) e y el valor de la ordenada (vertical).
y que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente:
Teorema La ecuación general de primer grado Ax + By + C = 0 , donde A, B, C pertenecen a los números reales ( |
2.– Ecuación principal de la recta
Esta es otra de las formas de representar la ecuación de la recta.
Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:
Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa (horizontal) e y el valor de la ordenada (vertical).
(x, y) = (Abscisa , Ordenada)
Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.
Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.
Ejemplo: El punto ( 7, 2 ) (el 7 en la abscisa x y el 2 en la ordenada y ) satisface la ecuación y = x – 5 , ya que al reemplazar queda
2 = 7 – 5 lo que resulta verdadero.
Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce , que se obtiene con la fórmula
Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.
Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.
Ejemplo: El punto ( 7, 2 ) (el 7 en la abscisa x y el 2 en la ordenada y ) satisface la ecuación y = x – 5 , ya que al reemplazar queda
2 = 7 – 5 lo que resulta verdadero.
Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce , que se obtiene con la fórmula
y = mx + n
que considera las siguientes variables: un punto ( x, y ), la pendiente ( m ) y el punto de intercepción en la ordenada ( n ), y es conocida como ecuación principal de la recta (conocida también como forma simplificada, como veremos luego).
Al representar la ecuación de la recta en su forma principal vemos que aparecieron dos nuevas variables: la m y la n , esto agrega a nuestra ecuación de la recta dos nuevos elementos que deben considerase al analizar o representar una recta: la pendiente (m) y el punto de intercepción (n) (también llamado intercepto ) en el eje de las ordenadas (y) .

Respecto a esto, en el gráfico de arriba, m representa la pendiente de la recta y permite obtener su grado de inclinación (en relación a la horizontal o abscisa), y n es el coeficiente de posición, el número que señala el punto donde la recta interceptará al eje de las ordenadas (y).
que considera las siguientes variables: un punto ( x, y ), la pendiente ( m ) y el punto de intercepción en la ordenada ( n ), y es conocida como ecuación principal de la recta (conocida también como forma simplificada, como veremos luego).
Al representar la ecuación de la recta en su forma principal vemos que aparecieron dos nuevas variables: la m y la n , esto agrega a nuestra ecuación de la recta dos nuevos elementos que deben considerase al analizar o representar una recta: la pendiente (m) y el punto de intercepción (n) (también llamado intercepto ) en el eje de las ordenadas (y) .
 |
Respecto a esto, en el gráfico de arriba, m representa la pendiente de la recta y permite obtener su grado de inclinación (en relación a la horizontal o abscisa), y n es el coeficiente de posición, el número que señala el punto donde la recta interceptará al eje de las ordenadas (y).
Forma simplificada de la ecuación de la recta
Si se conoce la pendiente m , y el punto donde la recta corta al eje de ordenadas es ( 0, b ) (corresponde a n en la fórmula principal ya vista), podemos deducir, partiendo de la ecuación de la recta de la forma
Forma simplificada de la ecuación de la recta
Si se conoce la pendiente m , y el punto donde la recta corta al eje de ordenadas es ( 0, b ) (corresponde a n en la fórmula principal ya vista), podemos deducir, partiendo de la ecuación de la recta de la forma
y − y 1 = m(x − x 1 )
y – b = m(x – 0)
y – b = mx
y = mx + b
Esta es una segunda forma de la ecuación principal de la recta (se la llama también forma explícita de la ecuación ) y se utiliza cuando se conocen la pendiente y la ordenada al origen (o intercepto), que llamaremos b ( no olvidemos que corresponde a la n en la primera forma de la ecuación principal). También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo cual indica que interceptará al eje y en el punto (0, 7) .
Conocida la fórmula de la ecuación principal (simplificada o explícita, como quieran llamarla) de la recta es posible obtener la ecuación de cualquier recta siempre que se nos den al menos dos variables de ella: puede ser la pendiente, puede ser un punto o puede ser el intercepto.
SEMANA 31 DE AGOSTO AL 04 DE SEPTIEMBREPENDIENTE DE UNA RECTA
La idea de la pendiente es algo que encuentras en la vida cotidiana. Piensa en un carrito bajando una rampa o subir las escaleras. La rampa y la escalera tienen una pendiente. Puedes describir la pendiente de la rampa o de las escaleras considerando el movimiento horizontal y vertical. En una conversación, usas las palabras “gradual” o “empinado” para describir una pendiente. En una pendiente gradual, casi todo el movimiento es horizontal. En una pendiente empinada, el movimiento vertical es mayor.
Definiendo la Pendiente
La definición matemática de la pendiente es muy similar a la de la vida diaria. En matemáticas, la pendiente se usa para describir la inclinación y dirección de rectas. Tan solo con mirar la gráfica de una recta, puedes saber algunas cosas sobre su pendiente, especialmente relativa a otras rectas graficadas en el mismo plano de coordenadas. Considera las gráficas de las tres rectas siguientes:
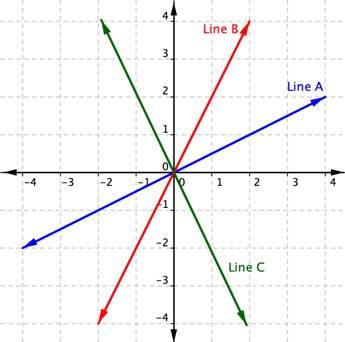
Primero, veamos las rectas A y B. Si imaginas que estas rectas son un cerro, dirías que la recta B es más empinada que la recta A. La recta B tiene una pendiente mayor que la recta A.
Ahora, observa que las rectas A y B se elevan conforme te mueves de izquierda a derecha. Decimos que estas rectas tienen una pendiente positiva. La recta C baja de izquierda a derecha por lo que tienen una pendiente negativa. Usando dos de los puntos en la recta, puedes calcular la pendiente de la recta encontrando la elevación y el avance. El cambio vertical entre dos puntos se llama elevación, y el cambio horizontal se llama avance. La pendiente es igual a la división de la elevación entre el avance: 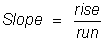 .
.
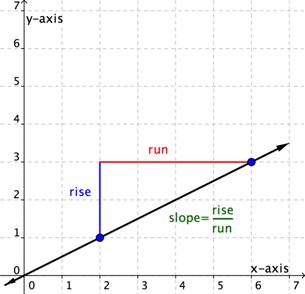
Puedes determinar la pendiente de una recta a partir de su gráfica examinando la elevación y el avance. Una característica de una recta es que su pendiente es constante en toda su extensión. Entonces, puedes escoger cualesquiera 2 puntos sobre la gráfica de la recta para calcular la pendiente. Veamos un ejemplo.
Ejemplo
Problema
Usa la gráfica para encontrar la pendiente de la recta.
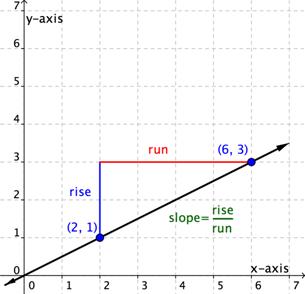
elevación = 2
Empieza en un punto en la recta, como (2, 1) y muévete verticalmente hasta alinearte con otro punto en la recta, como (6, 3). La elevación es de 2 unidades. Es positiva puesto que te moviste hacia arriba.
avance = 4
Luego, muévete horizontalmente al punto (6, 3). Cuenta el número de unidades. El avance es de 4 unidades. Es positivo puesto que te moviste hacia la derecha.
Pendiente = 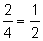
Pendiente = 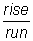 .
.
Respuesta
La pendiente es 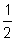 .
.
Esta recta tendrá una pendiente de 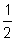 sin importar qué par de puntos hayas escogido de la recta. Intenta medir la pendiente partiendo del origen, (0, 0), al punto (6, 3). Encontrarás que la elevación = 3 y el avance = 6. La pendiente es
sin importar qué par de puntos hayas escogido de la recta. Intenta medir la pendiente partiendo del origen, (0, 0), al punto (6, 3). Encontrarás que la elevación = 3 y el avance = 6. La pendiente es 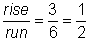 . ¡Es la misma!
. ¡Es la misma!
Veamos otro ejemplo.
Ejemplo
Problema
Usa la gráfica para encontrar la pendiente de la recta.
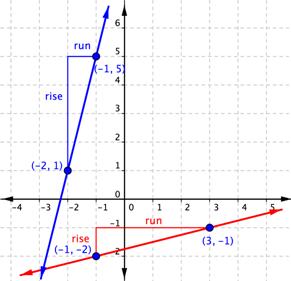
Observa que las dos rectas tienen pendientes positivas, por lo que esperamos que las respuestas sean positivas.
elevación = 4
Recta azul
Empieza con la recta azul, yendo del punto (-2, 1) al punto (-1, 5). Esta recta tiene una elevación de 4 unidades hacia arriba, por lo que es positiva.
avance = 1
El avance es de 1 unidad a la derecha, por lo que es positivo.
Pendiente = 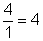
Sustituye los valores de la elevación y del avance y sustituye en la fórmula: Pendiente = 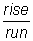 .
.
elevación = 1
Recta roja
La recta roja, va del punto (-1, -2) al punto (3, -1) tiene una elevación de 1 unidad.
avance = 4
La recta roja tiene un avance de 4 unidades.
Pendiente = 
Sustituye los valores de la elevación y del avance y sustituye en la fórmula: Pendiente = 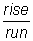 .
.
Respuesta
La pendiente de la recta azul es 4 y la pendiente de la recta roja es 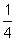 .
.
Cuando ves las dos rectas, puedes notar que la recta azul es más empinada que la recta roja. Tiene sentido que el valor de la pendiente de la recta azul, 4, es mayor que el valor de la pendiente de la recta roja, 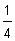 . Entra más grande es la pendiente, más empinada la recta.
. Entra más grande es la pendiente, más empinada la recta.
El siguiente ejemplo muestra una recta con una pendiente negativa.
Ejemplo
Problema
Usa la gráfica para encontrar la pendiente de la recta.
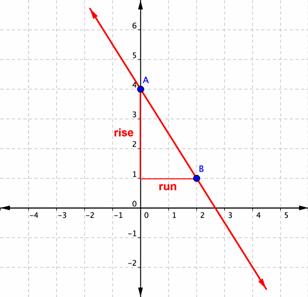
elevación = −3
Empieza en el punto A, (0, 4) y sube a −3. Esto significa que te mueves 3 unidades en la dirección negativa.
avance = 2
De ahí, avanza 2 unidades en la dirección positiva al punto B (2, 1).
Pendiente = 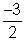
Pendiente = 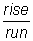 .
.
Respuesta
La pendiente de la recta es 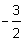 .
.
La dirección es importante cuando se trata de determinar la pendiente. Es importante poner atención a si te mueves hacia arriba, abajo, derecha, o izquierda; esto es, si te mueves en la dirección positiva o negativa. Si te mueves para arriba hacia el segundo punto, la elevación es positiva. Si te mueves para abajo hacia el segundo punto, la elevación es negativa. Si te mueves a la derecha hacia el segundo punto, el avance es positivo. Si te mueves a la izquierda hacia el segundo punto, el avance es negativo. En el ejemplo anterior, pudiste encontrar la pendiente empezando en el punto B, avanzando −2, y luego elevándote +3 para llegar al punto A. El resultado sigue siendo una pendiente de 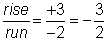 .
.
Ejemplo Avanzado
Problema
Encontrar la pendiente de la recta en la gráfica siguiente.
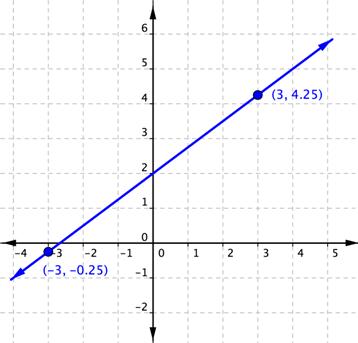
elevación = 4.5
Empieza en (-3, -0.25) y elévate 4.5. Esto significa que te mueves 4.5 unidades en la dirección positiva.
avance = 6
De ahí, muévete 6 unidades en la dirección positiva a (3, 4.25).

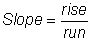
Respuesta
La pendiente de la recta es 0.75.
Estudiando Ecuaciones
A veces, la pendiente de una recta puede determinarse fácilmente de su ecuación. Consideremos la recta cuya ecuación es y = 5x. Puedes crear una tabla de valores para encontrar 3 puntos en la recta.
x
y
−1
−5
0
0
2
10
Usando los tres puntos, crea una gráfica de la recta y determina su pendiente.
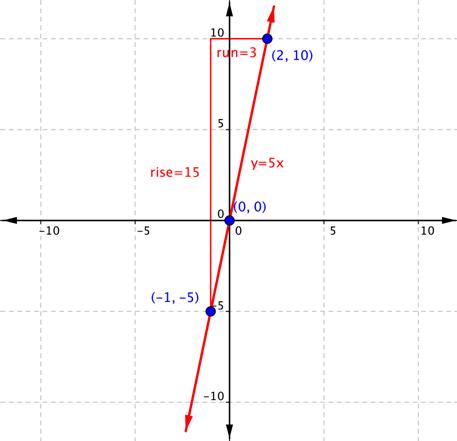
Conforme te mueves del punto (-1, -5) al punto (2, 10), la recta se eleva 15 y avanza 3, entonces la pendiente es 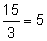 . Observa que el número 5 aparece en la ecuación: y = 5x.
. Observa que el número 5 aparece en la ecuación: y = 5x.
Siempre que la ecuación de la recta se escriba de la forma y = mx + b, se le llama la forma pendiente-intersección de la ecuación. La m es la pendiente de la recta. Y b es la be en el punto, es decir, la intersección en y(0, b).
Por ejemplo, en la ecuación y = 3x – 7, la pendiente es 3, y la intersección en y es (0, −7).
¿Y qué si la ecuación se escribe como 2y = 5x + 1? Entonces debes reescribir la ecuación en la forma y = mx + b. Despeja y.
2y = 5x + 1
y = 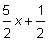 divide entre 2 ambos lados de la ecuación.
divide entre 2 ambos lados de la ecuación.
La pendiente es 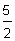 , y la intersección en y es (0,
, y la intersección en y es (0, 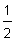 ).
).
SEMANA DEL 24 DE AGOSTO AL 29 DE AGOSTO
Esta es una segunda forma de la ecuación principal de la recta (se la llama también forma explícita de la ecuación ) y se utiliza cuando se conocen la pendiente y la ordenada al origen (o intercepto), que llamaremos b ( no olvidemos que corresponde a la n en la primera forma de la ecuación principal). También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo cual indica que interceptará al eje y en el punto (0, 7) .
Conocida la fórmula de la ecuación principal (simplificada o explícita, como quieran llamarla) de la recta es posible obtener la ecuación de cualquier recta siempre que se nos den al menos dos variables de ella: puede ser la pendiente, puede ser un punto o puede ser el intercepto.
La idea de la pendiente es algo que encuentras en la vida cotidiana. Piensa en un carrito bajando una rampa o subir las escaleras. La rampa y la escalera tienen una pendiente. Puedes describir la pendiente de la rampa o de las escaleras considerando el movimiento horizontal y vertical. En una conversación, usas las palabras “gradual” o “empinado” para describir una pendiente. En una pendiente gradual, casi todo el movimiento es horizontal. En una pendiente empinada, el movimiento vertical es mayor.
Definiendo la Pendiente
La definición matemática de la pendiente es muy similar a la de la vida diaria. En matemáticas, la pendiente se usa para describir la inclinación y dirección de rectas. Tan solo con mirar la gráfica de una recta, puedes saber algunas cosas sobre su pendiente, especialmente relativa a otras rectas graficadas en el mismo plano de coordenadas. Considera las gráficas de las tres rectas siguientes:

Primero, veamos las rectas A y B. Si imaginas que estas rectas son un cerro, dirías que la recta B es más empinada que la recta A. La recta B tiene una pendiente mayor que la recta A.
Ahora, observa que las rectas A y B se elevan conforme te mueves de izquierda a derecha. Decimos que estas rectas tienen una pendiente positiva. La recta C baja de izquierda a derecha por lo que tienen una pendiente negativa. Usando dos de los puntos en la recta, puedes calcular la pendiente de la recta encontrando la elevación y el avance. El cambio vertical entre dos puntos se llama elevación, y el cambio horizontal se llama avance. La pendiente es igual a la división de la elevación entre el avance: ![]() .
.

Puedes determinar la pendiente de una recta a partir de su gráfica examinando la elevación y el avance. Una característica de una recta es que su pendiente es constante en toda su extensión. Entonces, puedes escoger cualesquiera 2 puntos sobre la gráfica de la recta para calcular la pendiente. Veamos un ejemplo.
Ejemplo | ||
Problema | Usa la gráfica para encontrar la pendiente de la recta.
| |
| elevación = 2 | Empieza en un punto en la recta, como (2, 1) y muévete verticalmente hasta alinearte con otro punto en la recta, como (6, 3). La elevación es de 2 unidades. Es positiva puesto que te moviste hacia arriba. |
| avance = 4 | Luego, muévete horizontalmente al punto (6, 3). Cuenta el número de unidades. El avance es de 4 unidades. Es positivo puesto que te moviste hacia la derecha. |
| Pendiente = | Pendiente = |
Respuesta | La pendiente es |
|
Esta recta tendrá una pendiente de ![]() sin importar qué par de puntos hayas escogido de la recta. Intenta medir la pendiente partiendo del origen, (0, 0), al punto (6, 3). Encontrarás que la elevación = 3 y el avance = 6. La pendiente es
sin importar qué par de puntos hayas escogido de la recta. Intenta medir la pendiente partiendo del origen, (0, 0), al punto (6, 3). Encontrarás que la elevación = 3 y el avance = 6. La pendiente es ![]() . ¡Es la misma!
. ¡Es la misma!
Veamos otro ejemplo.
Ejemplo | ||||
Problema | Usa la gráfica para encontrar la pendiente de la recta.
|
| ||
|
| Observa que las dos rectas tienen pendientes positivas, por lo que esperamos que las respuestas sean positivas. | ||
|
elevación = 4 | Recta azul
Empieza con la recta azul, yendo del punto (-2, 1) al punto (-1, 5). Esta recta tiene una elevación de 4 unidades hacia arriba, por lo que es positiva. | ||
| avance = 1 | El avance es de 1 unidad a la derecha, por lo que es positivo. | ||
| Pendiente = | Sustituye los valores de la elevación y del avance y sustituye en la fórmula: Pendiente = | ||
|
elevación = 1 | Recta roja
La recta roja, va del punto (-1, -2) al punto (3, -1) tiene una elevación de 1 unidad. | ||
| avance = 4 | La recta roja tiene un avance de 4 unidades. | ||
| Pendiente = | Sustituye los valores de la elevación y del avance y sustituye en la fórmula: Pendiente = | ||
Respuesta | La pendiente de la recta azul es 4 y la pendiente de la recta roja es |
| ||
Cuando ves las dos rectas, puedes notar que la recta azul es más empinada que la recta roja. Tiene sentido que el valor de la pendiente de la recta azul, 4, es mayor que el valor de la pendiente de la recta roja, ![]() . Entra más grande es la pendiente, más empinada la recta.
. Entra más grande es la pendiente, más empinada la recta.
El siguiente ejemplo muestra una recta con una pendiente negativa.
Ejemplo | ||
Problema | Usa la gráfica para encontrar la pendiente de la recta.
| |
| elevación = −3 | Empieza en el punto A, (0, 4) y sube a −3. Esto significa que te mueves 3 unidades en la dirección negativa. |
| avance = 2 | De ahí, avanza 2 unidades en la dirección positiva al punto B (2, 1). |
| Pendiente = | Pendiente = |
Respuesta | La pendiente de la recta es | |
La dirección es importante cuando se trata de determinar la pendiente. Es importante poner atención a si te mueves hacia arriba, abajo, derecha, o izquierda; esto es, si te mueves en la dirección positiva o negativa. Si te mueves para arriba hacia el segundo punto, la elevación es positiva. Si te mueves para abajo hacia el segundo punto, la elevación es negativa. Si te mueves a la derecha hacia el segundo punto, el avance es positivo. Si te mueves a la izquierda hacia el segundo punto, el avance es negativo. En el ejemplo anterior, pudiste encontrar la pendiente empezando en el punto B, avanzando −2, y luego elevándote +3 para llegar al punto A. El resultado sigue siendo una pendiente de ![]() .
.
Ejemplo Avanzado | ||
Problema | Encontrar la pendiente de la recta en la gráfica siguiente.
| |
elevación = 4.5 | Empieza en (-3, -0.25) y elévate 4.5. Esto significa que te mueves 4.5 unidades en la dirección positiva. | |
avance = 6 | De ahí, muévete 6 unidades en la dirección positiva a (3, 4.25). | |
|
| |
Respuesta | La pendiente de la recta es 0.75. | |
Estudiando Ecuaciones
A veces, la pendiente de una recta puede determinarse fácilmente de su ecuación. Consideremos la recta cuya ecuación es y = 5x. Puedes crear una tabla de valores para encontrar 3 puntos en la recta.
x | y |
−1 | −5 |
0 | 0 |
2 | 10 |
Usando los tres puntos, crea una gráfica de la recta y determina su pendiente.

Conforme te mueves del punto (-1, -5) al punto (2, 10), la recta se eleva 15 y avanza 3, entonces la pendiente es ![]() . Observa que el número 5 aparece en la ecuación: y = 5x.
. Observa que el número 5 aparece en la ecuación: y = 5x.
Siempre que la ecuación de la recta se escriba de la forma y = mx + b, se le llama la forma pendiente-intersección de la ecuación. La m es la pendiente de la recta. Y b es la be en el punto, es decir, la intersección en y(0, b).
Por ejemplo, en la ecuación y = 3x – 7, la pendiente es 3, y la intersección en y es (0, −7).
¿Y qué si la ecuación se escribe como 2y = 5x + 1? Entonces debes reescribir la ecuación en la forma y = mx + b. Despeja y.
2y = 5x + 1
y = ![]() divide entre 2 ambos lados de la ecuación.
divide entre 2 ambos lados de la ecuación.
La pendiente es ![]() , y la intersección en y es (0,
, y la intersección en y es (0, ![]() ).
).
SISTEMA DE ECUACIONES DE 3 INCÓGNITAS CON TRES ECUACIONES, USANDO DETERMINANTES
DETERMINANTES DE ORDEN 3
DETERMINANTES DE 3ER ORDEN
Las matrices de orden 3 o matrices 3×3 son aquellas que tienen tres filas y tres columnas:
Para calcular el determinante de este tipo de matriz, utilizamos el Regla de Sarrus, que consiste en repetir las dos primeras columnas inmediatamente después de la tercera:
Luego siga los pasos a continuación:
1) Calcular la multiplicación diagonal. Para hacerlo, dibujamos flechas diagonales que facilitan el cálculo.
Las primeras flechas se dibujan de izquierda a derecha y corresponden a la diagonal principal:
1 * 5 * 8 = 40
2 * 6 * 2 = 24
3 * 2 * 5 = 30
2) Calculamos la multiplicación en el otro lado de la diagonal. Entonces dibujamos nuevas flechas.
Ahora las flechas se dibujan de derecha a izquierda y corresponden a la diagonal secundaria:
2 * 2 * 8 = 32
1 * 6 * 5 = 30
3 * 5 * 2 = 30
3) Agregamos cada uno de ellos:
40 + 24 + 30 = 94
32 + 30 + 30 = 92
4) Restamos cada uno de estos resultados:
94 – 92 = 2
Leer matrices y determinantes y, para comprender cómo calcular los determinantes de la matriz de orden 4 o superior, lea el teorema de Laplace.
Para calcular el determinante de una matriz cuadrada de orden 3 usaremos la «Regla de Sarrus».

Para calcularlo necesitamos sumar 6 productos (3 normales y otros 3 cambiados de signo).
Los tres primeros productos en la dirección de la diagonal principal
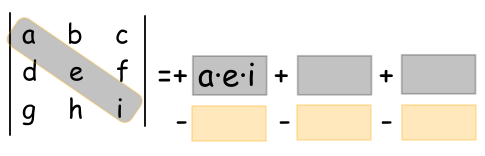

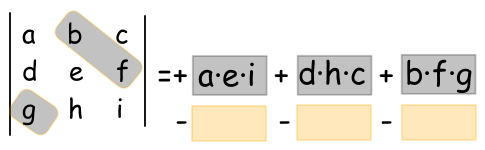
Los tres productos siguientes van cambiados de signo y en la dirección de la diagonal secundaria



Ejemplo



Las matrices de orden 3 o matrices 3×3 son aquellas que tienen tres filas y tres columnas:
Para calcular el determinante de este tipo de matriz, utilizamos el Regla de Sarrus, que consiste en repetir las dos primeras columnas inmediatamente después de la tercera:
Luego siga los pasos a continuación:
1) Calcular la multiplicación diagonal. Para hacerlo, dibujamos flechas diagonales que facilitan el cálculo.
Las primeras flechas se dibujan de izquierda a derecha y corresponden a la diagonal principal:
1 * 5 * 8 = 40
2 * 6 * 2 = 24
3 * 2 * 5 = 30
2) Calculamos la multiplicación en el otro lado de la diagonal. Entonces dibujamos nuevas flechas.
Ahora las flechas se dibujan de derecha a izquierda y corresponden a la diagonal secundaria:
2 * 2 * 8 = 32
1 * 6 * 5 = 30
3 * 5 * 2 = 30
3) Agregamos cada uno de ellos:
40 + 24 + 30 = 94
32 + 30 + 30 = 92
4) Restamos cada uno de estos resultados:
94 – 92 = 2
Leer matrices y determinantes y, para comprender cómo calcular los determinantes de la matriz de orden 4 o superior, lea el teorema de Laplace.
Para calcular el determinante de una matriz cuadrada de orden 3 usaremos la «Regla de Sarrus».

Para calcularlo necesitamos sumar 6 productos (3 normales y otros 3 cambiados de signo).
Los tres primeros productos en la dirección de la diagonal principal
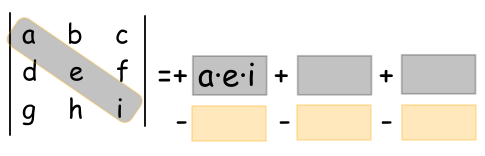


Los tres productos siguientes van cambiados de signo y en la dirección de la diagonal secundaria



Ejemplo

![]()

SEMANA DEL 10 DE AGOSTO AL 14 DE AGOSTO
RESOLVER UN SISTEMA DE ECUACIONES USANDO DETERMINANTES DE ORDEN 2
DETERMINANTES DE ORDEN 2SISTEMA DE ECUACIONES POR CRAMER
DETERMINANTES DE ORDEN 2 Sea A una matriz cuadrada de orden 2,
Se llama determinante de A al número real:

Es decir, el determinante de una matriz cuadrada de orden 2 es igual al producto de los elementos de la diagonal principal menos el producto de los elementos de la diagonal secundaria.
| DETERMINANTES DE ORDEN 2 |
| Sea A una matriz cuadrada de orden 2, Se llama determinante de A al número real: Es decir, el determinante de una matriz cuadrada de orden 2 es igual al producto de los elementos de la diagonal principal menos el producto de los elementos de la diagonal secundaria. |
La regla de Cramer proporciona la solución de sistemas de ecuaciones lineales compatibles determinados (con una única solución) mediante el cálculo de determinantes. Se trata de un método muy rápido para resolver sistemas, sobre todo, para sistemas de dimensión 2x2 y 3x3. Para dimensiones mayores, los determinantes son bastante más engorrosos.
Recordad que un sistema de ecuaciones puede escribirse en forma matricial como
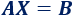
donde
es la matriz de coeficientes del sistema,
es la matriz con las incógnitas,
es la matriz con los términos independientes de las ecuaciones.
Para poder aplicar Cramer, la matriz tiene que ser cuadrada y regular (determinante distinto de 0).
La regla de Cramer establece que la incógnita de la solución del sistema, cuyos coeficientes están en la columna de , es
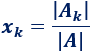
donde es como la matriz pero cambiando su columna número por la columna de términos independientes, .
La regla de Cramer proporciona la solución de sistemas de ecuaciones lineales compatibles determinados (con una única solución) mediante el cálculo de determinantes. Se trata de un método muy rápido para resolver sistemas, sobre todo, para sistemas de dimensión 2x2 y 3x3. Para dimensiones mayores, los determinantes son bastante más engorrosos.
Recordad que un sistema de ecuaciones puede escribirse en forma matricial como
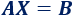
donde
es la matriz de coeficientes del sistema,
es la matriz con las incógnitas,
es la matriz con los términos independientes de las ecuaciones.
Para poder aplicar Cramer, la matriz tiene que ser cuadrada y regular (determinante distinto de 0).
La regla de Cramer establece que la incógnita de la solución del sistema, cuyos coeficientes están en la columna de , es
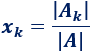
donde es como la matriz pero cambiando su columna número por la columna de términos independientes, .
Ejemplo 1
Sistema de dimensión 2x2:
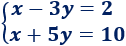
SoluciónLa matriz de coeficientes del sistema es
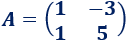
La matriz de incógnitas es
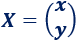
La matriz de términos independientes es
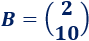
Calculamos el determinante de :
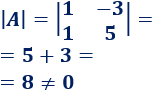
Podemos aplicar la regla de Cramer.
La primera incógnita es , cuyos coeficientes son los de la primera columna de . La matriz es como pero cambiando dicha columna por la columna :

Calculamos :
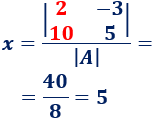
La segunda incógnita es y sus coeficientes son los de la segunda columna de . Tenemos que calcular el determinante de la matriz
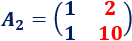
Calculamos :
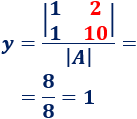
Por tanto, la solución del sistema es
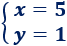
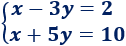
La matriz de coeficientes del sistema es
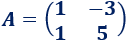
La matriz de incógnitas es
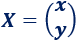
La matriz de términos independientes es
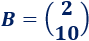
Calculamos el determinante de :
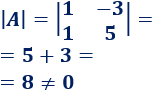
Podemos aplicar la regla de Cramer.
La primera incógnita es , cuyos coeficientes son los de la primera columna de . La matriz es como pero cambiando dicha columna por la columna :

Calculamos :
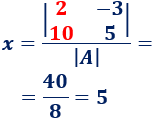
La segunda incógnita es y sus coeficientes son los de la segunda columna de . Tenemos que calcular el determinante de la matriz
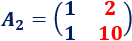
Calculamos :
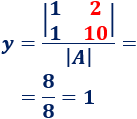
Por tanto, la solución del sistema es
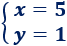
Ejemplo 2
Sistema de dimensión 2x2:
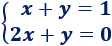
SoluciónLa matriz de coeficientes del sistema es
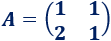
La matriz de términos independientes es
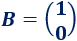
Calculamos el determinante de :
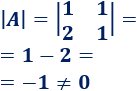
Podemos aplicar la regla de Cramer.
La matriz es
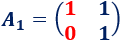
Calculamos :
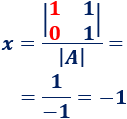
La matriz es
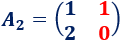
Calculamos :
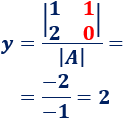
Por tanto, la solución del sistema es
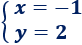
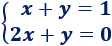
La matriz de coeficientes del sistema es
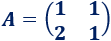
La matriz de términos independientes es
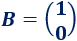
Calculamos el determinante de :
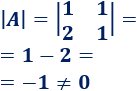
Podemos aplicar la regla de Cramer.
La matriz es
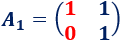
Calculamos :
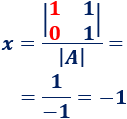
La matriz es
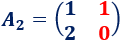
Calculamos :
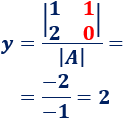
Por tanto, la solución del sistema es
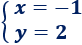
Ejemplo 3
Sistema de dimensión 3x3:
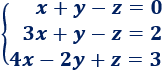
SoluciónLa matriz de coeficientes del sistema es

La matriz de incógnitas es
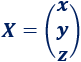
La matriz de términos independientes es
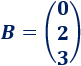
Calculamos el determinante de :
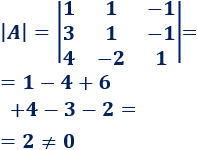
Podemos aplicar la regla de Cramer.
La matriz es como pero cambiando la columna 1 por la columna :

Calculamos :
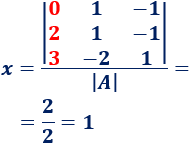
La matriz es como pero cambiando la columna 2 por la columna :

Calculamos :
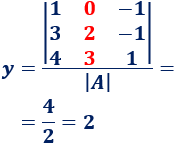
La matriz es como pero cambiando la columna 3 por la columna :
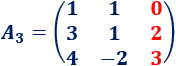
Calculamos :
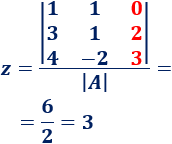
Por tanto, la solución del sistema es
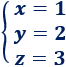
SEMANA DEL 27 DE JULIO AL 31 DE JULIO
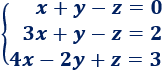
La matriz de coeficientes del sistema es

La matriz de incógnitas es
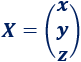
La matriz de términos independientes es
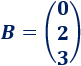
Calculamos el determinante de :
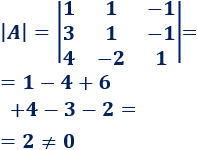
Podemos aplicar la regla de Cramer.
La matriz es como pero cambiando la columna 1 por la columna :

Calculamos :
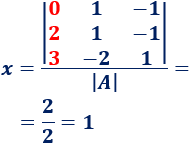
La matriz es como pero cambiando la columna 2 por la columna :

Calculamos :
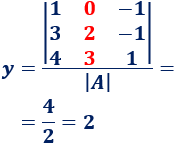
La matriz es como pero cambiando la columna 3 por la columna :
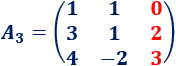
Calculamos :
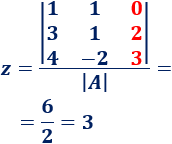
Por tanto, la solución del sistema es
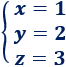
SISTEMA DE ECUACIONES MÉTODO DE ELIMINACIÓN
El método de eliminación para resolver sistemas de ecuaciones lineales usa la propiedad de la igualdad de la suma. Puedes sumar el mismo valor a cada lado de la ecuación.
Entonces si tienes un sistema: x – 6 = −6 y x + y = 8, puedes sumar x + y al lado izquierdo de la primera ecuación y suma 8 a la derecha de la ecuación. Y como x + y = 8, estas sumando el mismo valor a cada lado de la primera ecuación.
Si sumas las dos ecuaciones, x – y = −6 y x + y = 8 como explicamos arriba, observa lo que pasa.
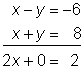
Has eliminado el término y y esta ecuación puede resolverse usando los métodos para resolver ecuaciones con una variable.
Veamos cómo se resuelve este sistema usando el método de eliminación.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
x – y = −6
x + y = 8
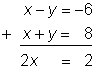
Suma las ecuaciones.
2x = 2
x = 1
Resuelve x.
x + y = 8
1 + y = 8
y = 8 – 1
y = 7
Sustituye x = 1 en una de las ecuaciones originales y resuelve y.
x – y = −6
1 – 7 = −6
−6 = −6
VÁLIDO
x + y = 8
1 + 7 = 8
8 = 8
VÁLIDO
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
Respuesta
La solución es (1, 7).
Desafortunadamente no todos los sistemas resultan tan fáciles. Por ejemplo, un sistema como 2x + y = 12 y −3x + y = 2. Si usamos estas ecuaciones, no se elimina ninguna variable.
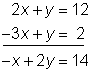
Pero quieres eliminar una variable. Por lo que sumas el opuesto de una de las ecuaciones con la otra ecuación.
2x + y =12 → 2x + y = 12 → 2x + y = 12
−3x + y = 2 → − (−3x + y) = −(2) → 3x – y = −2
5x + 0y = 10
Has eliminado la variable y, y ahora el problema puede resolverse. Veamos el ejemplo siguiente.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
2x + y = 12
−3x + y = 2
2x + y = 12
−3x + y = 2
Puedes eliminar la variable y si sumas el opuesto de una de las ecuaciones a la otra ecuación.
2x + y = 12
3x – y = −2
5x = 10
Reescribe la segunda ecuación como su opuesto.
Suma.
x = 2
Resuelve x.
2(2) + y = 12
4 + y = 12
y = 8
Sustituye y = 2 en una de las ecuaciones originales y resuelve y.
2x + y = 12
2(2) + 8 = 12
4 + 8 = 12
12 = 12
VÁLIDO
−3x + y = 2
−3(2) + 8 = 2
−6 + 8 = 2
2 = 2
VÁLIDO
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
Respuesta
La solución es (2, 8).
Los siguientes son dos ejemplos mostrando cómo resolver un sistema lineal de ecuaciones usando eliminación.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
−2x + 3y = −1
2x + 5y = 25
−2x
+
3y
=
−1
2x
+
5y
=
25
Observa los coeficientes de cada variable en la ecuación. Si sumas estas dos ecuaciones, el término x será eliminado porque −2x + 2x = 0.
−2x
+
3y
=
−1
2x
+
5y
=
25
8y
=
24
y
=
3
Suma y resuelve y.
2x + 5y = 25
2x + 5(3) = 25
2x + 15 = 25
2x = 10
x = 5
Sustituye y = 3 en una de las ecuaciones originales.
−2x + 3y = −1
−2(5) + 3(3) = −1
−10 + 9 = −1
−1 = −1
VÁLIDO
2x + 5y = 25
2(5) + 5(3) = 25
10 + 15 = 25
25 = 25
VÁLIDO
Comprueba las soluciones.
Los resultados son correctos.
Respuesta
La solución es (5, 3).
Ejemplo
Problema
Usa eliminación para resolver x y y.
4x + 2y = 14
5x + 2y = 16
4x
+
2y
=
14
5x
+
2y
=
16
Observa los coeficientes de cada variable en cada ecuación. Necesitarás sumar el opuesto de una de las ecuaciones para eliminar la variable y, porque 2y + 2y = 4y, pero
2y + (−2y) = 0.
4x
+
2y
=
14
−5x
–
2y
=
−16
−x
=
−2
x
=
2
Cambia una de las ecuaciones por su opuesto, suma y resuelve x.
4x + 2y = 14
4(2) + 2y = 14
8 + 2y = 14
2y = 6
y = 3
Sustituye x = 2 en una de las ecuaciones originales y resuelve y.
Respuesta
La solución es (2, 3).
Comprueba el último ejemplo — sustituye (2, 3) en ambas ecuaciones. Obtienes dos enunciados válidos: 14 = 14 y 16 = 16!
Observa que pudiste haber usado el opuesto de la primera ecuación en lugar del de la segunda ecuación y obtenido el mismo resultado.
Muchas veces, sumar las ecuaciones o sumar el opuesto de una de las ecuaciones no resultará en la eliminación de una variable. Observa el sistema siguiente.
3x + 4y = 52
5x + y = 30
Si sumas las ecuaciones anteriores o si sumas el opuesto de una de las ecuaciones, obtendrás una ecuación que sigue teniendo dos variables. Entonces, primero usemos la propiedad multiplicativa de la igualdad. Puedes multiplicar ambos lados de las ecuaciones por un número que hará que el coeficiente de una de las variables quede opuesto a la misma variable en la otra ecuación.
Es aquí donde la multiplicación es útil. Observa que la primera ecuación contiene el término 4y, y la segunda ecuación contiene el término y. Si multiplicas la segunda ecuación por −4, cuando sumes las dos ecuaciones las variables y se sumarán para ser 0.
3x + 4y = 52 → 3x + 4y = 52 → 3x + 4y = 52
5x + y = 30 → −4(5x + y) = −4(30) → −20x – 4y = −120
−17x + 0y = −68
Veamos el siguiente ejemplo.
Ejemplo
Problema
Resuelve x y y.
Ecuación A: 3x + 4y = 52
Ecuación B: 5x + y = 30
3x
+
4y
=
52
5x
+
y
=
30
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes.
3x
+
4y
=
52
−4(
5x
+
y)
=
−4
(30)
Multiplica la segunda ecuación por −4 para que tengan el mismo coeficiente.
3x
+
4y
=
52
−20x
–
4y
=
−120
Reescribe el sistema y suma las ecuaciones.
−17x
=
-68
x
=
4
Resuelve x.
3x + 4y = 52
3(4) + 4y = 52
12 + 4y = 52
4y = 40
y = 10
Sustituye x = 4 en una de las ecuaciones originales para encontrar y.
3x + 4y = 52
3(4) + 4(10) = 52
12 + 40 = 52
52 = 52
VÁLIDO
5x + y = 30
5(4) + 10 = 30
20 + 10 = 30
30 = 30
VÁLIDO
Comprueba tu respuesta.
Los resultados son correctos.
Respuesta
La solución es (4, 10).
Existen otras maneras de resolver este problema. En lugar de multiplicar una ecuación para eliminar una variable cuando las ecuaciones se suman, pudiste haber multiplicado ambas ecuaciones por números distintos.
Ahora eliminemos la variable x. Multiplica la Ecuación A por 5 y la Ecuación B por −3.
Ejemplo
Problema
Resuelve x y y.
3x + 4y = 52
5x + y = 30
3x
+
4y
=
52
5x
+
y
=
30
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes
5
(3x
+
4y)
=
5
(52)
5x
+
y
=
0
15x
+
20y
=
260
5x
+
y
=
30
Para usar el método de eliminación, debes crear variables con el mismo coeficiente, luego puedes multiplicarlas. Multiplica la primera ecuación por 5.
15x
+
20y
=
260
-3 (5x
+
y)
=
−3
(30)
15x
+
20y
=
260
−15x
–
3y
=
−90
Ahora multiplica la segunda ecuación −3.
15x
+
20y
=
+
260
−15x
–
3y
=
–
90
17y
=
170
y
=
10
Luego suma las ecuaciones, y resuelve y.
3x + 4y = 52
3x + 4(10) = 52
3x + 40 = 52
3x = 12
x = 4
Sustituye y = 10 en una de las ecuaciones originales para encontrar x.
Respuesta
La solución es (4, 10).
Llegas a la misma solución que antes.
Estas ecuaciones fueron multiplicadas por 5 y −3 respectivamente, porque eso te daba los términos que suman 0. Asegúrate de multiplicar todos los términos de la ecuación.
Félix necesita encontrar x y y del siguiente sistema.
Ecuación A: 7y − 4x = 5
Ecuación B: 3y + 4x = 25
Si quiere usar el método de eliminación para eliminar una de las variables, ¿cuál es la manera más eficiente de hacerlo?
A) Sumar la Ecuación A y la Ecuación B
B) Sumar 4x a ambos lados de la Ecuación A
C) Multiplicar la Ecuación A por 5
D) Multiplicar la Ecuación B por −1
Al igual que con el método de sustitución, el método de eliminación a veces elimina ambas variables y te quedas con un enunciado válido o inválido. Recuerda que un enunciado inválido significa que no hay solución.
Veamos otro ejemplo.
Ejemplo
Problema
Resuelve x y y.
-x – y = -4
x + y = 2
-x – y = -4
x + y = 2
0 = −2
Suma las ecuaciones para eliminar el término x.
Respuesta
No hay solución.
Graficar estas rectas muestra que son paralelas y como tales no comparten ningún punto, verificando que no hay solución.
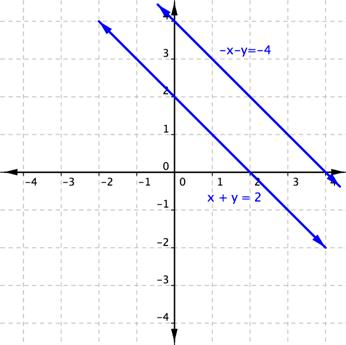
Si ambas variables son eliminadas y te quedas con un enunciado válido, significa que hay un número infinito de pares ordenados que satisfacen ambas ecuaciones. De hecho, las ecuaciones son la misma recta.
Ejemplo
Problema
Resuelve x y y.
x + y = 2
-x − y = -2
x + y = 2
-x − y = -2
0 = 0
Suma las ecuaciones para eliminar el término x.
Respuesta
Hay un número infinito de soluciones.
Graficar estas dos ecuaciones te ayudará a ilustrar lo que está sucediendo.
El método de eliminación puede aplicarse para resolver sistemas de ecuaciones que modelan situaciones del mundo real. Dos ejemplos del uso del método de eliminación se muestran a continuación.
Ejemplo
Problema
La suma de dos números es 10. La resta es 6. ¿Cuáles son estos números?
x + y = 10
x – y = 6
Escribe un sistema de ecuaciones para modelar la situación.
x = un número
y = el otro número
x + y = 10
+ x – y = 6
2x = 16
x = 8
Suma las ecuaciones para eliminar el término y y luego resolver x.
x + y = 10
8 + y = 10
y = 2
Sustituye el valor por x en una de las ecuaciones originales para encontrar y.
x + y = 10
8 + 2 = 10
10 = 10
VÁLIDO
x – y = 6
8 – 2 = 6
6 = 6
VÁLIDO
Comprueba tu respuesta sustituyendo x = 8 y y = 2 en el sistema original.
Los resultados son correctos.
Respuesta
Los números son 8 y 2.
Ejemplo
Problema
Un teatro vendió 800 boletos para el espectáculo del viernes en la noche. Un boleto de niño cuesta $4.50 y un boleto de adulto cuesta $6.00. LA cantidad total recolectada fue de $4,500. ¿Cuantos boletos de vendieron de cada tipo?
El número total de boletos vendidos es 800.
a + c = 800
La cantidad de dinero recolectado es $4,500
6a + 4.5c = 4,500
Sistema de ecuaciones:
a + c = 800
6a + 4.5c = 4,500
Escribe un sistema de ecuaciones para modelar la situación de la venta de boletos.
a = número de boletos de adulto vendidos
c = número de boletos de niño vendidos
6(a + c) = 6(800)
6a + 4.5c = 4,500
6a + 6c = 4,800
6a + 4.5c = 4,500
Usa la multiplicación para reescribir la primera ecuación.
6a + 6c = 4,800
−6a – 4.5c = −4,500
1.5c = 300
c = 200
Suma el opuesto de la segunda ecuación para eliminar el término y resolver c.
a + 200 = 800
−200 −200
a = 600
Sustituye 200 por c en una de las ecuaciones originales.
a + c = 800
600 + 200 = 800
800 = 800
VÁLIDO
6a + 4.5c = 4,500
6(600) + 4.5(200) = 4,500
3,600 + 900 = 4,500
4500 = 4,500
VÁLIDO
Comprueba tu respuesta sustituyendo
a = 600 y
c = 200 en el sistema original. Los resultados son correctos.
Respuesta
Se vendieron 600 boletos de adulto y 200 boletos de niño.
SEMANA DEL 20 DE JULIO AL 24 DE JULIO
El método de eliminación para resolver sistemas de ecuaciones lineales usa la propiedad de la igualdad de la suma. Puedes sumar el mismo valor a cada lado de la ecuación.
Entonces si tienes un sistema: x – 6 = −6 y x + y = 8, puedes sumar x + y al lado izquierdo de la primera ecuación y suma 8 a la derecha de la ecuación. Y como x + y = 8, estas sumando el mismo valor a cada lado de la primera ecuación.
Si sumas las dos ecuaciones, x – y = −6 y x + y = 8 como explicamos arriba, observa lo que pasa.
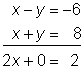
Has eliminado el término y y esta ecuación puede resolverse usando los métodos para resolver ecuaciones con una variable.
Veamos cómo se resuelve este sistema usando el método de eliminación.
Ejemplo | ||||
Problema | Usa eliminación para resolver el sistema. x – y = −6 x + y = 8 |
| ||
|
| Suma las ecuaciones. | ||
| 2x = 2 x = 1 | Resuelve x. | ||
| x + y = 8 1 + y = 8 y = 8 – 1 y = 7 | Sustituye x = 1 en una de las ecuaciones originales y resuelve y. | ||
| x – y = −6 1 – 7 = −6 −6 = −6
VÁLIDO | x + y = 8 1 + 7 = 8 8 = 8
VÁLIDO | ¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos. | |
Respuesta | La solución es (1, 7). |
| ||
Desafortunadamente no todos los sistemas resultan tan fáciles. Por ejemplo, un sistema como 2x + y = 12 y −3x + y = 2. Si usamos estas ecuaciones, no se elimina ninguna variable.
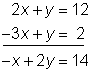
Pero quieres eliminar una variable. Por lo que sumas el opuesto de una de las ecuaciones con la otra ecuación.
2x + y =12 → 2x + y = 12 → 2x + y = 12
−3x + y = 2 → − (−3x + y) = −(2) → 3x – y = −2
5x + 0y = 10
Has eliminado la variable y, y ahora el problema puede resolverse. Veamos el ejemplo siguiente.
Ejemplo | ||||
Problema | Usa eliminación para resolver el sistema. 2x + y = 12 −3x + y = 2 |
| ||
| 2x + y = 12 −3x + y = 2 | Puedes eliminar la variable y si sumas el opuesto de una de las ecuaciones a la otra ecuación. | ||
| 2x + y = 12 3x – y = −2 5x = 10 | Reescribe la segunda ecuación como su opuesto. Suma. | ||
| x = 2 | Resuelve x. | ||
| 2(2) + y = 12 4 + y = 12 y = 8 | Sustituye y = 2 en una de las ecuaciones originales y resuelve y. | ||
| 2x + y = 12 2(2) + 8 = 12 4 + 8 = 12 12 = 12
VÁLIDO | −3x + y = 2 −3(2) + 8 = 2 −6 + 8 = 2 2 = 2
VÁLIDO | ¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos. | |
Respuesta | La solución es (2, 8). |
| ||
Los siguientes son dos ejemplos mostrando cómo resolver un sistema lineal de ecuaciones usando eliminación.
Ejemplo | |||||||||||||||||||||||||||||||||||
Problema | Usa eliminación para resolver el sistema. −2x + 3y = −1 2x + 5y = 25 | ||||||||||||||||||||||||||||||||||
|
| Observa los coeficientes de cada variable en la ecuación. Si sumas estas dos ecuaciones, el término x será eliminado porque −2x + 2x = 0. | |||||||||||||||||||||||||||||||||
|
| Suma y resuelve y. | |||||||||||||||||||||||||||||||||
| 2x + 5y = 25 2x + 5(3) = 25 2x + 15 = 25 2x = 10 x = 5 | Sustituye y = 3 en una de las ecuaciones originales. | |||||||||||||||||||||||||||||||||
| −2x + 3y = −1 −2(5) + 3(3) = −1 −10 + 9 = −1 −1 = −1
VÁLIDO | 2x + 5y = 25 2(5) + 5(3) = 25 10 + 15 = 25 25 = 25
VÁLIDO | Comprueba las soluciones.
Los resultados son correctos. | ||||||||||||||||||||||||||||||||
Respuesta | La solución es (5, 3). |
| |||||||||||||||||||||||||||||||||
Ejemplo | ||||||||||||||||||||||||||||
Problema | Usa eliminación para resolver x y y. 4x + 2y = 14 5x + 2y = 16 |
| ||||||||||||||||||||||||||
|
| Observa los coeficientes de cada variable en cada ecuación. Necesitarás sumar el opuesto de una de las ecuaciones para eliminar la variable y, porque 2y + 2y = 4y, pero 2y + (−2y) = 0. | ||||||||||||||||||||||||||
|
| Cambia una de las ecuaciones por su opuesto, suma y resuelve x.
| ||||||||||||||||||||||||||
| 4x + 2y = 14 4(2) + 2y = 14 8 + 2y = 14 2y = 6 y = 3 | Sustituye x = 2 en una de las ecuaciones originales y resuelve y. | ||||||||||||||||||||||||||
Respuesta | La solución es (2, 3). |
| ||||||||||||||||||||||||||
Comprueba el último ejemplo — sustituye (2, 3) en ambas ecuaciones. Obtienes dos enunciados válidos: 14 = 14 y 16 = 16!
Observa que pudiste haber usado el opuesto de la primera ecuación en lugar del de la segunda ecuación y obtenido el mismo resultado.
Muchas veces, sumar las ecuaciones o sumar el opuesto de una de las ecuaciones no resultará en la eliminación de una variable. Observa el sistema siguiente.
3x + 4y = 52
5x + y = 30
Si sumas las ecuaciones anteriores o si sumas el opuesto de una de las ecuaciones, obtendrás una ecuación que sigue teniendo dos variables. Entonces, primero usemos la propiedad multiplicativa de la igualdad. Puedes multiplicar ambos lados de las ecuaciones por un número que hará que el coeficiente de una de las variables quede opuesto a la misma variable en la otra ecuación.
Es aquí donde la multiplicación es útil. Observa que la primera ecuación contiene el término 4y, y la segunda ecuación contiene el término y. Si multiplicas la segunda ecuación por −4, cuando sumes las dos ecuaciones las variables y se sumarán para ser 0.
3x + 4y = 52 → 3x + 4y = 52 → 3x + 4y = 52
5x + y = 30 → −4(5x + y) = −4(30) → −20x – 4y = −120
−17x + 0y = −68
Veamos el siguiente ejemplo.
Ejemplo | |||||||||||||||||||
Problema | Resuelve x y y. Ecuación A: 3x + 4y = 52 Ecuación B: 5x + y = 30 | ||||||||||||||||||
|
| Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes.
| |||||||||||||||||
|
| Multiplica la segunda ecuación por −4 para que tengan el mismo coeficiente. | |||||||||||||||||
|
| Reescribe el sistema y suma las ecuaciones. | |||||||||||||||||
|
| Resuelve x. | |||||||||||||||||
| 3x + 4y = 52 3(4) + 4y = 52 12 + 4y = 52 4y = 40 y = 10 | Sustituye x = 4 en una de las ecuaciones originales para encontrar y. | |||||||||||||||||
| 3x + 4y = 52 3(4) + 4(10) = 52 12 + 40 = 52 52 = 52
VÁLIDO | 5x + y = 30 5(4) + 10 = 30 20 + 10 = 30 30 = 30
VÁLIDO | Comprueba tu respuesta.
Los resultados son correctos. | ||||||||||||||||
Respuesta | La solución es (4, 10). |
| |||||||||||||||||
Existen otras maneras de resolver este problema. En lugar de multiplicar una ecuación para eliminar una variable cuando las ecuaciones se suman, pudiste haber multiplicado ambas ecuaciones por números distintos.
Ahora eliminemos la variable x. Multiplica la Ecuación A por 5 y la Ecuación B por −3.
Ejemplo | |||||||||||||||||||||||||||||||
Problema | Resuelve x y y. 3x + 4y = 52 5x + y = 30 |
| |||||||||||||||||||||||||||||
|
| Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes
| |||||||||||||||||||||||||||||
|
| Para usar el método de eliminación, debes crear variables con el mismo coeficiente, luego puedes multiplicarlas. Multiplica la primera ecuación por 5. | |||||||||||||||||||||||||||||
|
| Ahora multiplica la segunda ecuación −3. | |||||||||||||||||||||||||||||
|
| Luego suma las ecuaciones, y resuelve y. | |||||||||||||||||||||||||||||
| 3x + 4y = 52 3x + 4(10) = 52 3x + 40 = 52 3x = 12 x = 4 | Sustituye y = 10 en una de las ecuaciones originales para encontrar x. | |||||||||||||||||||||||||||||
Respuesta | La solución es (4, 10). | Llegas a la misma solución que antes. | |||||||||||||||||||||||||||||
Estas ecuaciones fueron multiplicadas por 5 y −3 respectivamente, porque eso te daba los términos que suman 0. Asegúrate de multiplicar todos los términos de la ecuación.
Félix necesita encontrar x y y del siguiente sistema. Ecuación A: 7y − 4x = 5 Ecuación B: 3y + 4x = 25
Si quiere usar el método de eliminación para eliminar una de las variables, ¿cuál es la manera más eficiente de hacerlo?
A) Sumar la Ecuación A y la Ecuación B
B) Sumar 4x a ambos lados de la Ecuación A
C) Multiplicar la Ecuación A por 5
D) Multiplicar la Ecuación B por −1
|
Al igual que con el método de sustitución, el método de eliminación a veces elimina ambas variables y te quedas con un enunciado válido o inválido. Recuerda que un enunciado inválido significa que no hay solución.
Veamos otro ejemplo.
Ejemplo | ||
Problema | Resuelve x y y. -x – y = -4 x + y = 2 |
|
| -x – y = -4 x + y = 2 0 = −2 | Suma las ecuaciones para eliminar el término x. |
Respuesta | No hay solución. |
|
Graficar estas rectas muestra que son paralelas y como tales no comparten ningún punto, verificando que no hay solución.

Si ambas variables son eliminadas y te quedas con un enunciado válido, significa que hay un número infinito de pares ordenados que satisfacen ambas ecuaciones. De hecho, las ecuaciones son la misma recta.
Ejemplo | ||
Problema | Resuelve x y y. x + y = 2 -x − y = -2 |
|
x + y = 2 -x − y = -2 0 = 0 | Suma las ecuaciones para eliminar el término x. | |
Respuesta | Hay un número infinito de soluciones. | |
Graficar estas dos ecuaciones te ayudará a ilustrar lo que está sucediendo.
El método de eliminación puede aplicarse para resolver sistemas de ecuaciones que modelan situaciones del mundo real. Dos ejemplos del uso del método de eliminación se muestran a continuación.
Ejemplo | |||
Problema | La suma de dos números es 10. La resta es 6. ¿Cuáles son estos números? | ||
| x + y = 10 x – y = 6 | Escribe un sistema de ecuaciones para modelar la situación. x = un número y = el otro número | |
| x + y = 10 + x – y = 6 2x = 16 x = 8 | Suma las ecuaciones para eliminar el término y y luego resolver x. | |
| x + y = 10 8 + y = 10 y = 2 | Sustituye el valor por x en una de las ecuaciones originales para encontrar y. | |
| x + y = 10 8 + 2 = 10 10 = 10
VÁLIDO | x – y = 6 8 – 2 = 6 6 = 6
VÁLIDO | Comprueba tu respuesta sustituyendo x = 8 y y = 2 en el sistema original.
Los resultados son correctos. |
Respuesta | Los números son 8 y 2. | ||
Ejemplo | ||||
Problema | Un teatro vendió 800 boletos para el espectáculo del viernes en la noche. Un boleto de niño cuesta $4.50 y un boleto de adulto cuesta $6.00. LA cantidad total recolectada fue de $4,500. ¿Cuantos boletos de vendieron de cada tipo? | |||
| El número total de boletos vendidos es 800. a + c = 800 La cantidad de dinero recolectado es $4,500 6a + 4.5c = 4,500
Sistema de ecuaciones: a + c = 800 6a + 4.5c = 4,500 | Escribe un sistema de ecuaciones para modelar la situación de la venta de boletos. a = número de boletos de adulto vendidos c = número de boletos de niño vendidos | ||
| 6(a + c) = 6(800) 6a + 4.5c = 4,500
6a + 6c = 4,800 6a + 4.5c = 4,500 | Usa la multiplicación para reescribir la primera ecuación.
| ||
| 6a + 6c = 4,800 −6a – 4.5c = −4,500 1.5c = 300
c = 200 | Suma el opuesto de la segunda ecuación para eliminar el término y resolver c. | ||
| a + 200 = 800 −200 −200 a = 600 | Sustituye 200 por c en una de las ecuaciones originales. | ||
| a + c = 800 600 + 200 = 800 800 = 800
VÁLIDO
| 6a + 4.5c = 4,500 6(600) + 4.5(200) = 4,500 3,600 + 900 = 4,500 4500 = 4,500
VÁLIDO | Comprueba tu respuesta sustituyendo a = 600 y c = 200 en el sistema original. Los resultados son correctos. | |
Respuesta | Se vendieron 600 boletos de adulto y 200 boletos de niño. |
| ||
SISTEMA DE ECUACIONES MÉTODO DE SUSTITUCIÓN
Básicamente, el método de sustitución consiste en:
- Despejar una incógnita en una de las ecuaciones, que quedará en función de la otra incógnita (seguiremos teniendo una ecuación).
- En la otra ecuación que no hemos utilizado, se sustituye la misma incógnita por el valor obtenido en el paso 1.
- Despejar la única incógnita que nos quede. Obtenemos el valor numérico de una incógnita.
- Sustituir la incógnita despejada en el paso 3 por su valor numérico (también obtenido en el paso 3) en la ecuación obtenida en el paso 1.
- Operar para obtener el valor numérico de la otra incógnita.
Vamos a resolver por ejemplo el siguiente sistema de ecuaciones:

Para saber en todo momento a qué ecuación del sistema nos referimos, a la ecuación de arriba le llamaremos primera ecuación y a la de abajo segunda ecuación:

1- Despejamos una incógnita en una de las ecuaciones, teniendo en cuenta las reglas de la transposición de términos.
La más fácil para despejar es la «y» en la primera ecuación, ya que no tiene ningún número delante y además tiene un signo más delante, por lo que tan sólo pasando el 5x al otro lado ya tenemos la y despejada:

Este es de momento nuestro valor de y, que decimos que está en función de x, porque x está contenida en su resultado. Además, la destacamos encerrándola en un recuadro rojo, porque más tarde tendremos que volver a esta ecuación.
2- En la ecuación que no hemos utilizado, sustituimos la misma incógnita despejada en el paso anterior, por el valor que hemos obtenido.
Es decir, en la segunda ecuación, donde aparece y, lo sustituimos por su valor en función de x:

Nos queda un ecuación que solamente depende de una incógnita.
3 – Despejamos la incógnita que nos queda.
Ahora tenemos una ecuación que depende sólo de x. Si necesitas ayuda con las ecuaciones de primer grado, dentro de mis cursos, puedes encontrar el Curso de Ecuaciones de Primer Grado, donde explico muy detalladamente cómo resolver ecuaciones de primer grado, con ejercicios resueltos y propuestos para practicar.
Resolvemos la ecuación que nos ha quedado.
En primer lugar, eliminamos el paréntesis cambiando de signo a los términos que estaban dentro:

Dejamos en el primer miembro los términos con x y pasamos al segundo miembro los términos que no llevan x:

Operamos en ambos miembros:
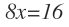
Despejamos la x, pasando el 8 dividiendo al segundo miembro:

Operamos en el segundo miembro y obtenemos el valor numérico de x:

4 – El valor numérico obtenido se sustituye en la ecuación donde despejamos una incógnita en función de otra (paso 1). En nuestro caso, donde despejamos y en función de x:

Sustituimos la x por su valor:
5 – Y operamos para obtener el valor numérico de la incógnita que nos queda:

Por tanto, la solución de este sistema es x=2, y=-2.
Básicamente, el método de sustitución consiste en:
- Despejar una incógnita en una de las ecuaciones, que quedará en función de la otra incógnita (seguiremos teniendo una ecuación).
- En la otra ecuación que no hemos utilizado, se sustituye la misma incógnita por el valor obtenido en el paso 1.
- Despejar la única incógnita que nos quede. Obtenemos el valor numérico de una incógnita.
- Sustituir la incógnita despejada en el paso 3 por su valor numérico (también obtenido en el paso 3) en la ecuación obtenida en el paso 1.
- Operar para obtener el valor numérico de la otra incógnita.
Vamos a resolver por ejemplo el siguiente sistema de ecuaciones:

Para saber en todo momento a qué ecuación del sistema nos referimos, a la ecuación de arriba le llamaremos primera ecuación y a la de abajo segunda ecuación:

1- Despejamos una incógnita en una de las ecuaciones, teniendo en cuenta las reglas de la transposición de términos.
La más fácil para despejar es la «y» en la primera ecuación, ya que no tiene ningún número delante y además tiene un signo más delante, por lo que tan sólo pasando el 5x al otro lado ya tenemos la y despejada:
![]()
Este es de momento nuestro valor de y, que decimos que está en función de x, porque x está contenida en su resultado. Además, la destacamos encerrándola en un recuadro rojo, porque más tarde tendremos que volver a esta ecuación.
2- En la ecuación que no hemos utilizado, sustituimos la misma incógnita despejada en el paso anterior, por el valor que hemos obtenido.
Es decir, en la segunda ecuación, donde aparece y, lo sustituimos por su valor en función de x:
![]()
Nos queda un ecuación que solamente depende de una incógnita.
3 – Despejamos la incógnita que nos queda.
Ahora tenemos una ecuación que depende sólo de x. Si necesitas ayuda con las ecuaciones de primer grado, dentro de mis cursos, puedes encontrar el Curso de Ecuaciones de Primer Grado, donde explico muy detalladamente cómo resolver ecuaciones de primer grado, con ejercicios resueltos y propuestos para practicar.
Resolvemos la ecuación que nos ha quedado.
En primer lugar, eliminamos el paréntesis cambiando de signo a los términos que estaban dentro:
![]()
Dejamos en el primer miembro los términos con x y pasamos al segundo miembro los términos que no llevan x:
![]()
Operamos en ambos miembros:
![]()
Despejamos la x, pasando el 8 dividiendo al segundo miembro:

Operamos en el segundo miembro y obtenemos el valor numérico de x:
![]()
4 – El valor numérico obtenido se sustituye en la ecuación donde despejamos una incógnita en función de otra (paso 1). En nuestro caso, donde despejamos y en función de x:
![]()
Sustituimos la x por su valor:![]()
5 – Y operamos para obtener el valor numérico de la incógnita que nos queda:

Por tanto, la solución de este sistema es x=2, y=-2.
Ejercicios resueltos de sistemas de ecuaciones por el método de sustitución
Para que te quede más claro, vamos a resolver sistemas de ecuaciones con dos incógnitas con el método de sustitución paso a paso
Para que te quede más claro, vamos a resolver sistemas de ecuaciones con dos incógnitas con el método de sustitución paso a paso
Ejercicio 1
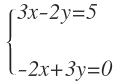
De la primera ecuación:

Vamos a despejar la x, ya que tiene signo positivo y resulta más sencillo despejarla.
Primer pasamos 2y sumando al segundo miembro:
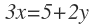
Y después pasamos el 3 dividiendo:

Por lo que ya tenemos la x despejada.
Ahora, en la segunda ecuación:
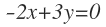
Sustituimos la x por el valor que acabamos de calcular:
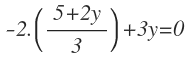
Y empezamos a operar. En primer lugar, multiplicamos el -2 por el numerador de la fracción (mucho cuidado con los signos):

Ahora reducimos a denominador común el primer miembro (el segundo miembro no es necesario porque tenemos un cero):

Eliminamos el denominador y nos queda:
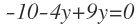
Pasamos el 10 al segundo miembro y operamos en el primer miembro:
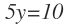
Y despejamos la «y»:
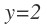
Este valor de «y», los sustituimos en la expresión donde despejamos la x:
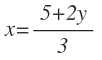
Nos queda:

Y operando obtenemos también el valor de x:
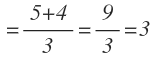
Por tanto, la solución del sistema es:

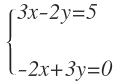
De la primera ecuación:
![]()
Vamos a despejar la x, ya que tiene signo positivo y resulta más sencillo despejarla.
Primer pasamos 2y sumando al segundo miembro:
![]()
Y después pasamos el 3 dividiendo:

Por lo que ya tenemos la x despejada.
Ahora, en la segunda ecuación:
![]()
Sustituimos la x por el valor que acabamos de calcular:
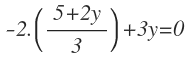
Y empezamos a operar. En primer lugar, multiplicamos el -2 por el numerador de la fracción (mucho cuidado con los signos):

Ahora reducimos a denominador común el primer miembro (el segundo miembro no es necesario porque tenemos un cero):

Eliminamos el denominador y nos queda:
![]()
Pasamos el 10 al segundo miembro y operamos en el primer miembro:
![]()
Y despejamos la «y»:
![]()
Este valor de «y», los sustituimos en la expresión donde despejamos la x:
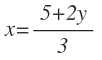
Nos queda:

Y operando obtenemos también el valor de x:
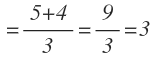
Por tanto, la solución del sistema es:
![]()
Ejercicio 2
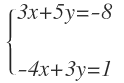
En la primera ecuación:

Despejamos la x, ya que tiene signo positivo.
Para ello primero pasamos el 5y restando al segundo miembro:

Y después pasamos el 3 dividiendo:
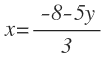
En la segunda ecuación:

Sustituimos la x por el valor obtenido de x:

Multiplicamos el numerador de la fracción por el -4 que tiene delante, teniendo en cuenta los signos:
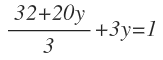
Reducimos los términos de ambos miembros a denominador común:

Eliminamos paréntesis de ambos miembros:

Dejamos en el primer miembro los términos con «y» y en el segundo miembro los términos sin «y» y operamos:
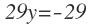
Finalmente hallamos el valor de «y»:
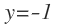
En la expresión que hallamos para la x:

Sustituimos la «y» por su valor numérico:
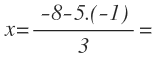
Operamos y obtenemos el valor de x:
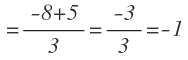
Por lo que la solución del sistema es:

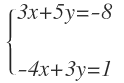
En la primera ecuación:
![]()
Despejamos la x, ya que tiene signo positivo.
Para ello primero pasamos el 5y restando al segundo miembro:
![]()
Y después pasamos el 3 dividiendo:
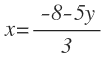
En la segunda ecuación:
![]()
Sustituimos la x por el valor obtenido de x:

Multiplicamos el numerador de la fracción por el -4 que tiene delante, teniendo en cuenta los signos:
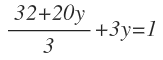
Reducimos los términos de ambos miembros a denominador común:

Eliminamos paréntesis de ambos miembros:
![]()
Dejamos en el primer miembro los términos con «y» y en el segundo miembro los términos sin «y» y operamos:
![]()
Finalmente hallamos el valor de «y»:
![]()
En la expresión que hallamos para la x:

Sustituimos la «y» por su valor numérico:
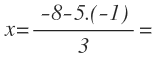
Operamos y obtenemos el valor de x:
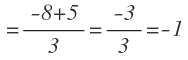
Por lo que la solución del sistema es:
![]()
Método de sustitución: Cuando conviene utilizarlo
El método de sustitución es el más utilizado de los tres, ya que es el más polivalente. Utilízalo si no te indican lo contrario en tus ejercicios.
Por cierto, si quieres aprender a resolver sistemas de ecuaciones con el método de igualación o el método de reducción, te recuerdo que tienes a tu disposición el Curso de Sistemas de dos Ecuaciones con dos Incógnitas. También aprenderás por qué a veces un sistema no tiene solución, por ejemplo.
Por tanto, a la pregunta de ¿cuándo tengo que utilizar el método de sustitución? La respuesta es que cuando no tengas claro qué método utilizar, utiliza el método de sustitución. En el 95% de los casos.
El método de sustitución es el más utilizado de los tres, ya que es el más polivalente. Utilízalo si no te indican lo contrario en tus ejercicios.
Por cierto, si quieres aprender a resolver sistemas de ecuaciones con el método de igualación o el método de reducción, te recuerdo que tienes a tu disposición el Curso de Sistemas de dos Ecuaciones con dos Incógnitas. También aprenderás por qué a veces un sistema no tiene solución, por ejemplo.
Por tanto, a la pregunta de ¿cuándo tengo que utilizar el método de sustitución? La respuesta es que cuando no tengas claro qué método utilizar, utiliza el método de sustitución. En el 95% de los casos.
SEMANA DEL 30 DE JUNIO AL 03 DE JULIO
SISTEMA DE ECUACIONES LINEALES POR IGUALACIÓN
¿Cuales son los pasos de resolución por el método de igualación?
1 Despejamos la misma incógnita en ambas ecuaciones
2 Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3 Resolvemos la ecuación
4 Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1 Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2 Igualamos las expresiones:

3 Resolvemos la ecuación:






4 Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5 Solución:


 de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:









 ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









SEMANA 22 AL 26 DE JUNIO
SISTEMA DE ECUACIONES LINEALES POR IGUALACIÓN
¿Cuales son los pasos de resolución por el método de igualación?
1 Despejamos la misma incógnita en ambas ecuaciones
2 Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3 Resolvemos la ecuación
4 Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1 Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2 Igualamos las expresiones:

3 Resolvemos la ecuación:






4 Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5 Solución:


 de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:









 ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









SEMANA 15 AL 19 DE JUNIO
SISTEMA DE ECUACIONES LINEALES POR IGUALACIÓN
¿Cuales son los pasos de resolución por el método de igualación?
1 Despejamos la misma incógnita en ambas ecuaciones
2 Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3 Resolvemos la ecuación
4 Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1 Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2 Igualamos las expresiones:

3 Resolvemos la ecuación:






4 Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5 Solución:


 de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:









 ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









SEMANA 08 AL 12 DE JUNIO
SISTEMA DE ECUACIONES LINEALES POR IGUALACIÓN
¿Cuales son los pasos de resolución por el método de igualación?
1 Despejamos la misma incógnita en ambas ecuaciones
2 Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3 Resolvemos la ecuación
4 Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1 Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2 Igualamos las expresiones:

3 Resolvemos la ecuación:






4 Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5 Solución:


 de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:









 ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









SEMANA 01 AL 05 DE JUNIO
SISTEMA DE ECUACIONES LINEALES POR IGUALACIÓN
SEMANA 01 AL 05 DE JUNIO
¿Cuales son los pasos de resolución por el método de igualación?
1 Despejamos la misma incógnita en ambas ecuaciones
2 Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3 Resolvemos la ecuación
4 Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1 Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2 Igualamos las expresiones:

3 Resolvemos la ecuación:






4 Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5 Solución:


 de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:









 ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









SEMANA 25 AL 29 DE MAYO
SISTEMA DE ECUACIONES LINEALES POR IGUALACIÓN
SEMANA 25 AL 29 DE MAYO
¿Cuales son los pasos de resolución por el método de igualación?
1 Despejamos la misma incógnita en ambas ecuaciones
2 Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3 Resolvemos la ecuación
4 Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1 Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2 Igualamos las expresiones:

3 Resolvemos la ecuación:






4 Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5 Solución:


 de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:









 ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









SEMANA 18 AL 22 DE MAYO
SISTEMA DE ECUACIONES LINEALES POR IGUALACIÓN
SEMANA 18 AL 22 DE MAYO
¿Cuales son los pasos de resolución por el método de igualación?
1 Despejamos la misma incógnita en ambas ecuaciones
2 Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3 Resolvemos la ecuación
4 Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 Los dos valores obtenidos constituyen la solución del sistema
Ejemplo de sistema de ecuaciones resuelto por el método de igualación

1 Despejamos, por ejemplo, la incógnita  de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:



2 Igualamos las expresiones:

3 Resolvemos la ecuación:






4 Sustituimos el valor de y, en cualquiera de las  ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









5 Solución:

SEMANA 11 AL 15 DE MAYO
SISTEMA DE ECUACIONES LINEALES POR ELIMINACIÓN
(REPLANIFICACIÓN)
El método de eliminación para resolver sistemas de ecuaciones lineales usa la propiedad de la igualdad de la suma. Puedes sumar el mismo valor a cada lado de la ecuación.
Entonces si tienes un sistema: x – 6 = −6 y x + y = 8, puedes sumar x + y al lado izquierdo de la primera ecuación y suma 8 a la derecha de la ecuación. Y como x + y = 8, estas sumando el mismo valor a cada lado de la primera ecuación.
Si sumas las dos ecuaciones, x – y = −6 y x + y = 8 como explicamos arriba, observa lo que pasa.
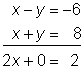
Has eliminado el término y y esta ecuación puede resolverse usando los métodos para resolver ecuaciones con una variable.
Veamos cómo se resuelve este sistema usando el método de eliminación.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
x – y = −6
x + y = 8
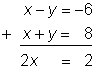
Suma las ecuaciones.
2x = 2
x = 1
Resuelve x.
x + y = 8
1 + y = 8
y = 8 – 1
y = 7
Sustituye x = 1 en una de las ecuaciones originales y resuelve y.
x – y = −6
1 – 7 = −6
−6 = −6
VÁLIDO
x + y = 8
1 + 7 = 8
8 = 8
VÁLIDO
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
Respuesta
La solución es (1, 7).
Desafortunadamente no todos los sistemas resultan tan fáciles. Por ejemplo, un sistema como 2x + y = 12 y −3x + y = 2. Si usamos estas ecuaciones, no se elimina ninguna variable.
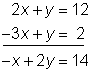
Pero quieres eliminar una variable. Por lo que sumas el opuesto de una de las ecuaciones con la otra ecuación.
2x + y =12 → 2x + y = 12 → 2x + y = 12
−3x + y = 2 → − (−3x + y) = −(2) → 3x – y = −2
5x + 0y = 10
Has eliminado la variable y, y ahora el problema puede resolverse. Veamos el ejemplo siguiente.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
2x + y = 12
−3x + y = 2
2x + y = 12
−3x + y = 2
Puedes eliminar la variable y si sumas el opuesto de una de las ecuaciones a la otra ecuación.
2x + y = 12
3x – y = −2
5x = 10
Reescribe la segunda ecuación como su opuesto.
Suma.
x = 2
Resuelve x.
2(2) + y = 12
4 + y = 12
y = 8
Sustituye y = 2 en una de las ecuaciones originales y resuelve y.
2x + y = 12
2(2) + 8 = 12
4 + 8 = 12
12 = 12
VÁLIDO
−3x + y = 2
−3(2) + 8 = 2
−6 + 8 = 2
2 = 2
VÁLIDO
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
Respuesta
La solución es (2, 8).
Los siguientes son dos ejemplos mostrando cómo resolver un sistema lineal de ecuaciones usando eliminación.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
−2x + 3y = −1
2x + 5y = 25
−2x
+
3y
=
−1
2x
+
5y
=
25
Observa los coeficientes de cada variable en la ecuación. Si sumas estas dos ecuaciones, el término x será eliminado porque −2x + 2x = 0.
−2x
+
3y
=
−1
2x
+
5y
=
25
8y
=
24
y
=
3
Suma y resuelve y.
2x + 5y = 25
2x + 5(3) = 25
2x + 15 = 25
2x = 10
x = 5
Sustituye y = 3 en una de las ecuaciones originales.
−2x + 3y = −1
−2(5) + 3(3) = −1
−10 + 9 = −1
−1 = −1
VÁLIDO
2x + 5y = 25
2(5) + 5(3) = 25
10 + 15 = 25
25 = 25
VÁLIDO
Comprueba las soluciones.
Los resultados son correctos.
Respuesta
La solución es (5, 3).
Ejemplo
Problema
Usa eliminación para resolver x y y.
4x + 2y = 14
5x + 2y = 16
4x
+
2y
=
14
5x
+
2y
=
16
Observa los coeficientes de cada variable en cada ecuación. Necesitarás sumar el opuesto de una de las ecuaciones para eliminar la variable y, porque 2y + 2y = 4y, pero
2y + (−2y) = 0.
4x
+
2y
=
14
−5x
–
2y
=
−16
−x
=
−2
x
=
2
Cambia una de las ecuaciones por su opuesto, suma y resuelve x.
4x + 2y = 14
4(2) + 2y = 14
8 + 2y = 14
2y = 6
y = 3
Sustituye x = 2 en una de las ecuaciones originales y resuelve y.
Respuesta
La solución es (2, 3).
Comprueba el último ejemplo — sustituye (2, 3) en ambas ecuaciones. Obtienes dos enunciados válidos: 14 = 14 y 16 = 16!
Observa que pudiste haber usado el opuesto de la primera ecuación en lugar del de la segunda ecuación y obtenido el mismo resultado.
Muchas veces, sumar las ecuaciones o sumar el opuesto de una de las ecuaciones no resultará en la eliminación de una variable. Observa el sistema siguiente.
3x + 4y = 52
5x + y = 30
Si sumas las ecuaciones anteriores o si sumas el opuesto de una de las ecuaciones, obtendrás una ecuación que sigue teniendo dos variables. Entonces, primero usemos la propiedad multiplicativa de la igualdad. Puedes multiplicar ambos lados de las ecuaciones por un número que hará que el coeficiente de una de las variables quede opuesto a la misma variable en la otra ecuación.
Es aquí donde la multiplicación es útil. Observa que la primera ecuación contiene el término 4y, y la segunda ecuación contiene el término y. Si multiplicas la segunda ecuación por −4, cuando sumes las dos ecuaciones las variables y se sumarán para ser 0.
3x + 4y = 52 → 3x + 4y = 52 → 3x + 4y = 52
5x + y = 30 → −4(5x + y) = −4(30) → −20x – 4y = −120
−17x + 0y = −68
Veamos el siguiente ejemplo.
Ejemplo
Problema
Resuelve x y y.
Ecuación A: 3x + 4y = 52
Ecuación B: 5x + y = 30
3x
+
4y
=
52
5x
+
y
=
30
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes.
3x
+
4y
=
52
−4(
5x
+
y)
=
−4
(30)
Multiplica la segunda ecuación por −4 para que tengan el mismo coeficiente.
3x
+
4y
=
52
−20x
–
4y
=
−120
Reescribe el sistema y suma las ecuaciones.
−17x
=
-68
x
=
4
Resuelve x.
3x + 4y = 52
3(4) + 4y = 52
12 + 4y = 52
4y = 40
y = 10
Sustituye x = 4 en una de las ecuaciones originales para encontrar y.
3x + 4y = 52
3(4) + 4(10) = 52
12 + 40 = 52
52 = 52
VÁLIDO
5x + y = 30
5(4) + 10 = 30
20 + 10 = 30
30 = 30
VÁLIDO
Comprueba tu respuesta.
Los resultados son correctos.
Respuesta
La solución es (4, 10).
Existen otras maneras de resolver este problema. En lugar de multiplicar una ecuación para eliminar una variable cuando las ecuaciones se suman, pudiste haber multiplicado ambas ecuaciones por números distintos.
Ahora eliminemos la variable x. Multiplica la Ecuación A por 5 y la Ecuación B por −3.
Ejemplo
Problema
Resuelve x y y.
3x + 4y = 52
5x + y = 30
3x
+
4y
=
52
5x
+
y
=
30
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes
5
(3x
+
4y)
=
5
(52)
5x
+
y
=
0
15x
+
20y
=
260
5x
+
y
=
30
Para usar el método de eliminación, debes crear variables con el mismo coeficiente, luego puedes multiplicarlas. Multiplica la primera ecuación por 5.
15x
+
20y
=
260
-3 (5x
+
y)
=
−3
(30)
15x
+
20y
=
260
−15x
–
3y
=
−90
Ahora multiplica la segunda ecuación −3.
15x
+
20y
=
+
260
−15x
–
3y
=
–
90
17y
=
170
y
=
10
Luego suma las ecuaciones, y resuelve y.
3x + 4y = 52
3x + 4(10) = 52
3x + 40 = 52
3x = 12
x = 4
Sustituye y = 10 en una de las ecuaciones originales para encontrar x.
Respuesta
La solución es (4, 10).
Llegas a la misma solución que antes.
Estas ecuaciones fueron multiplicadas por 5 y −3 respectivamente, porque eso te daba los términos que suman 0. Asegúrate de multiplicar todos los términos de la ecuación.
Félix necesita encontrar x y y del siguiente sistema.
Ecuación A: 7y − 4x = 5
Ecuación B: 3y + 4x = 25
Si quiere usar el método de eliminación para eliminar una de las variables, ¿cuál es la manera más eficiente de hacerlo?
A) Sumar la Ecuación A y la Ecuación B
B) Sumar 4x a ambos lados de la Ecuación A
C) Multiplicar la Ecuación A por 5
D) Multiplicar la Ecuación B por −1
SEMANA 4 AL 8 DE MAYO
SISTEMA DE ECUACIONES LINEALES POR ELIMINACIÓN
El método de eliminación para resolver sistemas de ecuaciones lineales usa la propiedad de la igualdad de la suma. Puedes sumar el mismo valor a cada lado de la ecuación.
Entonces si tienes un sistema: x – 6 = −6 y x + y = 8, puedes sumar x + y al lado izquierdo de la primera ecuación y suma 8 a la derecha de la ecuación. Y como x + y = 8, estas sumando el mismo valor a cada lado de la primera ecuación.
Si sumas las dos ecuaciones, x – y = −6 y x + y = 8 como explicamos arriba, observa lo que pasa.
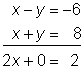
Has eliminado el término y y esta ecuación puede resolverse usando los métodos para resolver ecuaciones con una variable.
Veamos cómo se resuelve este sistema usando el método de eliminación.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
x – y = −6
x + y = 8
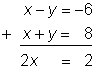
Suma las ecuaciones.
2x = 2
x = 1
Resuelve x.
x + y = 8
1 + y = 8
y = 8 – 1
y = 7
Sustituye x = 1 en una de las ecuaciones originales y resuelve y.
x – y = −6
1 – 7 = −6
−6 = −6
VÁLIDO
x + y = 8
1 + 7 = 8
8 = 8
VÁLIDO
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
Respuesta
La solución es (1, 7).
Desafortunadamente no todos los sistemas resultan tan fáciles. Por ejemplo, un sistema como 2x + y = 12 y −3x + y = 2. Si usamos estas ecuaciones, no se elimina ninguna variable.
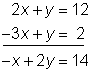
Pero quieres eliminar una variable. Por lo que sumas el opuesto de una de las ecuaciones con la otra ecuación.
2x + y =12 → 2x + y = 12 → 2x + y = 12
−3x + y = 2 → − (−3x + y) = −(2) → 3x – y = −2
5x + 0y = 10
Has eliminado la variable y, y ahora el problema puede resolverse. Veamos el ejemplo siguiente.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
2x + y = 12
−3x + y = 2
2x + y = 12
−3x + y = 2
Puedes eliminar la variable y si sumas el opuesto de una de las ecuaciones a la otra ecuación.
2x + y = 12
3x – y = −2
5x = 10
Reescribe la segunda ecuación como su opuesto.
Suma.
x = 2
Resuelve x.
2(2) + y = 12
4 + y = 12
y = 8
Sustituye y = 2 en una de las ecuaciones originales y resuelve y.
2x + y = 12
2(2) + 8 = 12
4 + 8 = 12
12 = 12
VÁLIDO
−3x + y = 2
−3(2) + 8 = 2
−6 + 8 = 2
2 = 2
VÁLIDO
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
Respuesta
La solución es (2, 8).
Los siguientes son dos ejemplos mostrando cómo resolver un sistema lineal de ecuaciones usando eliminación.
Ejemplo
Problema
Usa eliminación para resolver el sistema.
−2x + 3y = −1
2x + 5y = 25
−2x
+
3y
=
−1
2x
+
5y
=
25
Observa los coeficientes de cada variable en la ecuación. Si sumas estas dos ecuaciones, el término x será eliminado porque −2x + 2x = 0.
−2x
+
3y
=
−1
2x
+
5y
=
25
8y
=
24
y
=
3
Suma y resuelve y.
2x + 5y = 25
2x + 5(3) = 25
2x + 15 = 25
2x = 10
x = 5
Sustituye y = 3 en una de las ecuaciones originales.
−2x + 3y = −1
−2(5) + 3(3) = −1
−10 + 9 = −1
−1 = −1
VÁLIDO
2x + 5y = 25
2(5) + 5(3) = 25
10 + 15 = 25
25 = 25
VÁLIDO
Comprueba las soluciones.
Los resultados son correctos.
Respuesta
La solución es (5, 3).
Ejemplo
Problema
Usa eliminación para resolver x y y.
4x + 2y = 14
5x + 2y = 16
4x
+
2y
=
14
5x
+
2y
=
16
Observa los coeficientes de cada variable en cada ecuación. Necesitarás sumar el opuesto de una de las ecuaciones para eliminar la variable y, porque 2y + 2y = 4y, pero
2y + (−2y) = 0.
4x
+
2y
=
14
−5x
–
2y
=
−16
−x
=
−2
x
=
2
Cambia una de las ecuaciones por su opuesto, suma y resuelve x.
4x + 2y = 14
4(2) + 2y = 14
8 + 2y = 14
2y = 6
y = 3
Sustituye x = 2 en una de las ecuaciones originales y resuelve y.
Respuesta
La solución es (2, 3).
Comprueba el último ejemplo — sustituye (2, 3) en ambas ecuaciones. Obtienes dos enunciados válidos: 14 = 14 y 16 = 16!
Observa que pudiste haber usado el opuesto de la primera ecuación en lugar del de la segunda ecuación y obtenido el mismo resultado.
Muchas veces, sumar las ecuaciones o sumar el opuesto de una de las ecuaciones no resultará en la eliminación de una variable. Observa el sistema siguiente.
3x + 4y = 52
5x + y = 30
Si sumas las ecuaciones anteriores o si sumas el opuesto de una de las ecuaciones, obtendrás una ecuación que sigue teniendo dos variables. Entonces, primero usemos la propiedad multiplicativa de la igualdad. Puedes multiplicar ambos lados de las ecuaciones por un número que hará que el coeficiente de una de las variables quede opuesto a la misma variable en la otra ecuación.
Es aquí donde la multiplicación es útil. Observa que la primera ecuación contiene el término 4y, y la segunda ecuación contiene el término y. Si multiplicas la segunda ecuación por −4, cuando sumes las dos ecuaciones las variables y se sumarán para ser 0.
3x + 4y = 52 → 3x + 4y = 52 → 3x + 4y = 52
5x + y = 30 → −4(5x + y) = −4(30) → −20x – 4y = −120
−17x + 0y = −68
Veamos el siguiente ejemplo.
Ejemplo
Problema
Resuelve x y y.
Ecuación A: 3x + 4y = 52
Ecuación B: 5x + y = 30
3x
+
4y
=
52
5x
+
y
=
30
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes.
3x
+
4y
=
52
−4(
5x
+
y)
=
−4
(30)
Multiplica la segunda ecuación por −4 para que tengan el mismo coeficiente.
3x
+
4y
=
52
−20x
–
4y
=
−120
Reescribe el sistema y suma las ecuaciones.
−17x
=
-68
x
=
4
Resuelve x.
3x + 4y = 52
3(4) + 4y = 52
12 + 4y = 52
4y = 40
y = 10
Sustituye x = 4 en una de las ecuaciones originales para encontrar y.
3x + 4y = 52
3(4) + 4(10) = 52
12 + 40 = 52
52 = 52
VÁLIDO
5x + y = 30
5(4) + 10 = 30
20 + 10 = 30
30 = 30
VÁLIDO
Comprueba tu respuesta.
Los resultados son correctos.
Respuesta
La solución es (4, 10).
Existen otras maneras de resolver este problema. En lugar de multiplicar una ecuación para eliminar una variable cuando las ecuaciones se suman, pudiste haber multiplicado ambas ecuaciones por números distintos.
Ahora eliminemos la variable x. Multiplica la Ecuación A por 5 y la Ecuación B por −3.
Ejemplo
Problema
Resuelve x y y.
3x + 4y = 52
5x + y = 30
3x
+
4y
=
52
5x
+
y
=
30
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes
5
(3x
+
4y)
=
5
(52)
5x
+
y
=
0
15x
+
20y
=
260
5x
+
y
=
30
Para usar el método de eliminación, debes crear variables con el mismo coeficiente, luego puedes multiplicarlas. Multiplica la primera ecuación por 5.
15x
+
20y
=
260
-3 (5x
+
y)
=
−3
(30)
15x
+
20y
=
260
−15x
–
3y
=
−90
Ahora multiplica la segunda ecuación −3.
15x
+
20y
=
+
260
−15x
–
3y
=
–
90
17y
=
170
y
=
10
Luego suma las ecuaciones, y resuelve y.
3x + 4y = 52
3x + 4(10) = 52
3x + 40 = 52
3x = 12
x = 4
Sustituye y = 10 en una de las ecuaciones originales para encontrar x.
Respuesta
La solución es (4, 10).
Llegas a la misma solución que antes.
Estas ecuaciones fueron multiplicadas por 5 y −3 respectivamente, porque eso te daba los términos que suman 0. Asegúrate de multiplicar todos los términos de la ecuación.
Félix necesita encontrar x y y del siguiente sistema.
Ecuación A: 7y − 4x = 5
Ecuación B: 3y + 4x = 25
Si quiere usar el método de eliminación para eliminar una de las variables, ¿cuál es la manera más eficiente de hacerlo?
A) Sumar la Ecuación A y la Ecuación B
B) Sumar 4x a ambos lados de la Ecuación A
C) Multiplicar la Ecuación A por 5
D) Multiplicar la Ecuación B por −1
1. Función lineal
Una función lineal es aquella cuya expresión algebraica es del tipo y = mx,siendo m un número cualquiera distinto de 0.
- Su gráfica es una línea recta que pasa por el origen, (0,0).
- El número m se llama pendiente.
- La función es creciente si m > 0 y decreciente si m < 0.
Ejemplo: Vamos a representar gráficamente la función lineal y = 2x.Para ello, vamos a construir su tabla de valores, pero no debemos olvidar que su gráfica es una recta que pasa por el origen, por lo que bastará dar un valor a x y obtener su correspondiente de y. Después uniremos ese punto obtenido con el origen de coordenadas mediante una línea recta.Tabla de valores

 de la primera y de la segunda ecuación:
de la primera y de la segunda ecuación:









 ecuaciones (en cualquiera de las
ecuaciones (en cualquiera de las  , el resultado debe ser el mismo):
, el resultado debe ser el mismo):









(REPLANIFICACIÓN)
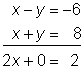
Ejemplo
| ||||
Problema
|
Usa eliminación para resolver el sistema.
x – y = −6
x + y = 8
| |||
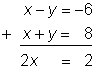 |
Suma las ecuaciones.
| |||
2x = 2
x = 1
|
Resuelve x.
| |||
x + y = 8
1 + y = 8
y = 8 – 1
y = 7
|
Sustituye x = 1 en una de las ecuaciones originales y resuelve y.
| |||
x – y = −6
1 – 7 = −6
−6 = −6
VÁLIDO
|
x + y = 8
1 + 7 = 8
8 = 8
VÁLIDO
|
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
| ||
Respuesta
|
La solución es (1, 7).
| |||
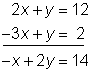
Ejemplo
| ||||
Problema
|
Usa eliminación para resolver el sistema.
2x + y = 12
−3x + y = 2
| |||
2x + y = 12
−3x + y = 2
|
Puedes eliminar la variable y si sumas el opuesto de una de las ecuaciones a la otra ecuación.
| |||
2x + y = 12
3x – y = −2
5x = 10
|
Reescribe la segunda ecuación como su opuesto.
Suma.
| |||
x = 2
|
Resuelve x.
| |||
2(2) + y = 12
4 + y = 12
y = 8
|
Sustituye y = 2 en una de las ecuaciones originales y resuelve y.
| |||
2x + y = 12
2(2) + 8 = 12
4 + 8 = 12
12 = 12
VÁLIDO
|
−3x + y = 2
−3(2) + 8 = 2
−6 + 8 = 2
2 = 2
VÁLIDO
|
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
| ||
Respuesta
|
La solución es (2, 8).
| |||
Ejemplo
| |||||||||||||||||||||||||||||||||||
Problema
|
Usa eliminación para resolver el sistema.
−2x + 3y = −1
2x + 5y = 25
| ||||||||||||||||||||||||||||||||||
|
Observa los coeficientes de cada variable en la ecuación. Si sumas estas dos ecuaciones, el término x será eliminado porque −2x + 2x = 0.
| ||||||||||||||||||||||||||||||||||
|
Suma y resuelve y.
| ||||||||||||||||||||||||||||||||||
2x + 5y = 25
2x + 5(3) = 25
2x + 15 = 25
2x = 10
x = 5
|
Sustituye y = 3 en una de las ecuaciones originales.
| ||||||||||||||||||||||||||||||||||
−2x + 3y = −1
−2(5) + 3(3) = −1
−10 + 9 = −1
−1 = −1
VÁLIDO
|
2x + 5y = 25
2(5) + 5(3) = 25
10 + 15 = 25
25 = 25
VÁLIDO
|
Comprueba las soluciones.
Los resultados son correctos.
| |||||||||||||||||||||||||||||||||
Respuesta
|
La solución es (5, 3).
| ||||||||||||||||||||||||||||||||||
Ejemplo
| ||||||||||||||||||||||||||||
Problema
|
Usa eliminación para resolver x y y.
4x + 2y = 14
5x + 2y = 16
| |||||||||||||||||||||||||||
|
Observa los coeficientes de cada variable en cada ecuación. Necesitarás sumar el opuesto de una de las ecuaciones para eliminar la variable y, porque 2y + 2y = 4y, pero
2y + (−2y) = 0.
| |||||||||||||||||||||||||||
|
Cambia una de las ecuaciones por su opuesto, suma y resuelve x.
| |||||||||||||||||||||||||||
4x + 2y = 14
4(2) + 2y = 14
8 + 2y = 14
2y = 6
y = 3
|
Sustituye x = 2 en una de las ecuaciones originales y resuelve y.
| |||||||||||||||||||||||||||
Respuesta
|
La solución es (2, 3).
| |||||||||||||||||||||||||||
Ejemplo
| |||||||||||||||||||
Problema
|
Resuelve x y y.
Ecuación A: 3x + 4y = 52
Ecuación B: 5x + y = 30
| ||||||||||||||||||
|
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes.
| ||||||||||||||||||
|
Multiplica la segunda ecuación por −4 para que tengan el mismo coeficiente.
| ||||||||||||||||||
|
Reescribe el sistema y suma las ecuaciones.
| ||||||||||||||||||
|
Resuelve x.
| ||||||||||||||||||
3x + 4y = 52
3(4) + 4y = 52
12 + 4y = 52
4y = 40
y = 10
|
Sustituye x = 4 en una de las ecuaciones originales para encontrar y.
| ||||||||||||||||||
3x + 4y = 52
3(4) + 4(10) = 52
12 + 40 = 52
52 = 52
VÁLIDO
|
5x + y = 30
5(4) + 10 = 30
20 + 10 = 30
30 = 30
VÁLIDO
|
Comprueba tu respuesta.
Los resultados son correctos.
| |||||||||||||||||
Respuesta
|
La solución es (4, 10).
| ||||||||||||||||||
Ejemplo
| |||||||||||||||||||||||||||||||
Problema
|
Resuelve x y y.
3x + 4y = 52
5x + y = 30
| ||||||||||||||||||||||||||||||
|
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes
| ||||||||||||||||||||||||||||||
|
Para usar el método de eliminación, debes crear variables con el mismo coeficiente, luego puedes multiplicarlas. Multiplica la primera ecuación por 5.
| ||||||||||||||||||||||||||||||
|
Ahora multiplica la segunda ecuación −3.
| ||||||||||||||||||||||||||||||
|
Luego suma las ecuaciones, y resuelve y.
| ||||||||||||||||||||||||||||||
3x + 4y = 52
3x + 4(10) = 52
3x + 40 = 52
3x = 12
x = 4
|
Sustituye y = 10 en una de las ecuaciones originales para encontrar x.
| ||||||||||||||||||||||||||||||
Respuesta
|
La solución es (4, 10).
|
Llegas a la misma solución que antes.
| |||||||||||||||||||||||||||||
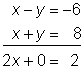
Ejemplo
| ||||
Problema
|
Usa eliminación para resolver el sistema.
x – y = −6
x + y = 8
| |||
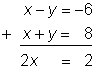 |
Suma las ecuaciones.
| |||
2x = 2
x = 1
|
Resuelve x.
| |||
x + y = 8
1 + y = 8
y = 8 – 1
y = 7
|
Sustituye x = 1 en una de las ecuaciones originales y resuelve y.
| |||
x – y = −6
1 – 7 = −6
−6 = −6
VÁLIDO
|
x + y = 8
1 + 7 = 8
8 = 8
VÁLIDO
|
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
| ||
Respuesta
|
La solución es (1, 7).
| |||
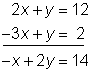
Ejemplo
| ||||
Problema
|
Usa eliminación para resolver el sistema.
2x + y = 12
−3x + y = 2
| |||
2x + y = 12
−3x + y = 2
|
Puedes eliminar la variable y si sumas el opuesto de una de las ecuaciones a la otra ecuación.
| |||
2x + y = 12
3x – y = −2
5x = 10
|
Reescribe la segunda ecuación como su opuesto.
Suma.
| |||
x = 2
|
Resuelve x.
| |||
2(2) + y = 12
4 + y = 12
y = 8
|
Sustituye y = 2 en una de las ecuaciones originales y resuelve y.
| |||
2x + y = 12
2(2) + 8 = 12
4 + 8 = 12
12 = 12
VÁLIDO
|
−3x + y = 2
−3(2) + 8 = 2
−6 + 8 = 2
2 = 2
VÁLIDO
|
¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos.
| ||
Respuesta
|
La solución es (2, 8).
| |||
Ejemplo
| |||||||||||||||||||||||||||||||||||
Problema
|
Usa eliminación para resolver el sistema.
−2x + 3y = −1
2x + 5y = 25
| ||||||||||||||||||||||||||||||||||
|
Observa los coeficientes de cada variable en la ecuación. Si sumas estas dos ecuaciones, el término x será eliminado porque −2x + 2x = 0.
| ||||||||||||||||||||||||||||||||||
|
Suma y resuelve y.
| ||||||||||||||||||||||||||||||||||
2x + 5y = 25
2x + 5(3) = 25
2x + 15 = 25
2x = 10
x = 5
|
Sustituye y = 3 en una de las ecuaciones originales.
| ||||||||||||||||||||||||||||||||||
−2x + 3y = −1
−2(5) + 3(3) = −1
−10 + 9 = −1
−1 = −1
VÁLIDO
|
2x + 5y = 25
2(5) + 5(3) = 25
10 + 15 = 25
25 = 25
VÁLIDO
|
Comprueba las soluciones.
Los resultados son correctos.
| |||||||||||||||||||||||||||||||||
Respuesta
|
La solución es (5, 3).
| ||||||||||||||||||||||||||||||||||
Ejemplo
| ||||||||||||||||||||||||||||
Problema
|
Usa eliminación para resolver x y y.
4x + 2y = 14
5x + 2y = 16
| |||||||||||||||||||||||||||
|
Observa los coeficientes de cada variable en cada ecuación. Necesitarás sumar el opuesto de una de las ecuaciones para eliminar la variable y, porque 2y + 2y = 4y, pero
2y + (−2y) = 0.
| |||||||||||||||||||||||||||
|
Cambia una de las ecuaciones por su opuesto, suma y resuelve x.
| |||||||||||||||||||||||||||
4x + 2y = 14
4(2) + 2y = 14
8 + 2y = 14
2y = 6
y = 3
|
Sustituye x = 2 en una de las ecuaciones originales y resuelve y.
| |||||||||||||||||||||||||||
Respuesta
|
La solución es (2, 3).
| |||||||||||||||||||||||||||
Ejemplo
| |||||||||||||||||||
Problema
|
Resuelve x y y.
Ecuación A: 3x + 4y = 52
Ecuación B: 5x + y = 30
| ||||||||||||||||||
|
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes.
| ||||||||||||||||||
|
Multiplica la segunda ecuación por −4 para que tengan el mismo coeficiente.
| ||||||||||||||||||
|
Reescribe el sistema y suma las ecuaciones.
| ||||||||||||||||||
|
Resuelve x.
| ||||||||||||||||||
3x + 4y = 52
3(4) + 4y = 52
12 + 4y = 52
4y = 40
y = 10
|
Sustituye x = 4 en una de las ecuaciones originales para encontrar y.
| ||||||||||||||||||
3x + 4y = 52
3(4) + 4(10) = 52
12 + 40 = 52
52 = 52
VÁLIDO
|
5x + y = 30
5(4) + 10 = 30
20 + 10 = 30
30 = 30
VÁLIDO
|
Comprueba tu respuesta.
Los resultados son correctos.
| |||||||||||||||||
Respuesta
|
La solución es (4, 10).
| ||||||||||||||||||
Ejemplo
| |||||||||||||||||||||||||||||||
Problema
|
Resuelve x y y.
3x + 4y = 52
5x + y = 30
| ||||||||||||||||||||||||||||||
|
Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes
| ||||||||||||||||||||||||||||||
|
Para usar el método de eliminación, debes crear variables con el mismo coeficiente, luego puedes multiplicarlas. Multiplica la primera ecuación por 5.
| ||||||||||||||||||||||||||||||
|
Ahora multiplica la segunda ecuación −3.
| ||||||||||||||||||||||||||||||
|
Luego suma las ecuaciones, y resuelve y.
| ||||||||||||||||||||||||||||||
3x + 4y = 52
3x + 4(10) = 52
3x + 40 = 52
3x = 12
x = 4
|
Sustituye y = 10 en una de las ecuaciones originales para encontrar x.
| ||||||||||||||||||||||||||||||
Respuesta
|
La solución es (4, 10).
|
Llegas a la misma solución que antes.
| |||||||||||||||||||||||||||||
| x | 1 |
| y | 2 |
- Su gráfica es una línea recta.
- El número m es la pendiente.
- El número n es la ordenada en el origen. La recta corta al eje Y en el punto (0,n).
Tabla de valores
| x | 1 |
| y | 1 |
a) y = 0,5x + 1 b) y = x + 2 c) y = 0,75x - 1
- Compara tus resultados con los que se obtienen al modificar el valor de m y n en la gráfica anterior.
- Si la recta pasa por el origen de coordenadas, es una función lineal, y = mx, y su pendiente, m, es la ordenada de x = 1.
- Si no pasa por el origen, es una función afín, y = mx + n, donde n es la ordenada de x = 0 y m es la ordenada de x = 1 menos n.
- Pasa por (0,-1), entonces n = -1.
- Pasa por (1,2), entonces m = 2 - n = 2 - (-1) = 3.

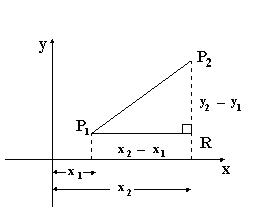








































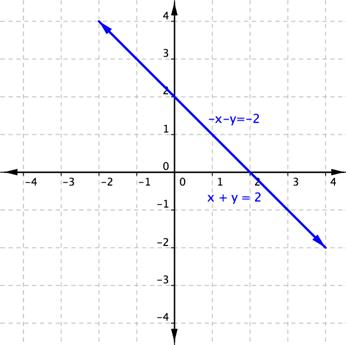


Buenas noches me podría indicar profesor a qué correo se envía la actividad de matemáticas de 9 grado
ResponderEliminar