MATEMÁTICA 6°
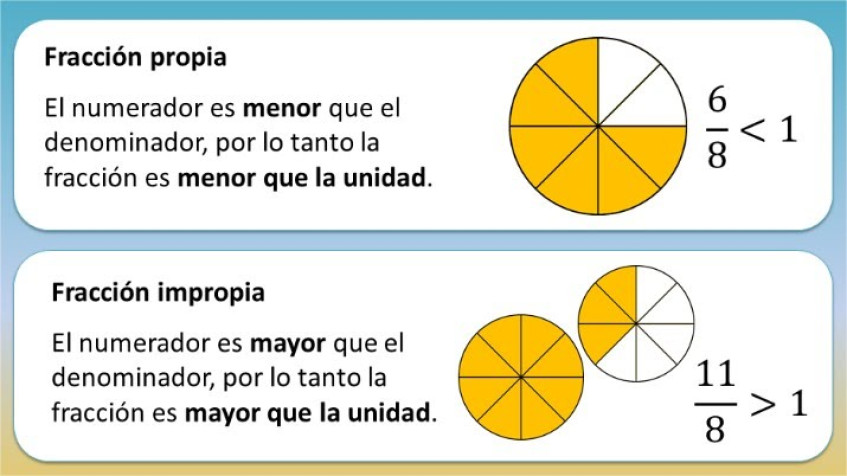
En muchas ocasiones encontrarás expresiones como , o . En estos casos debes tener en cuenta, además de los números, la intervención de los signos.
Para solucionar este tipo de situaciones primero debes recordar la ley de signos. Por si no la recuerdas, acá te la mostramos nuevamente, en la imagen de abajo la puedes observar:
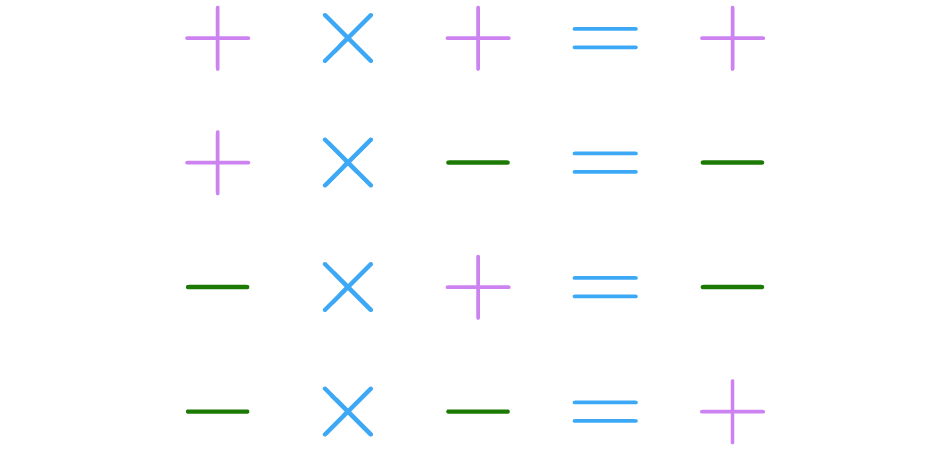
Cuando en una multiplicación intervengan signos, puedes usar primero la ley de signos para determinar el signo de la respuesta, después realiza el producto de los números como si los signos no estuvieran, ¿fácil, verdad?
Observa el siguiente ejemplo, multipliquemos los números: y :
Paso 1:
Recuerda que cuando un número no está precedido por ningún signo, se considera positivo. Por esta razón :
Paso 2:
Realiza la multiplicación de los números como ya sabes. En este caso . Por lo tanto el resultado de la multiplicación de menos tres y cinco es menos quince: . Obtendrás el mismo resultado si primero multiplicas los números y luego usas la ley de los signos.
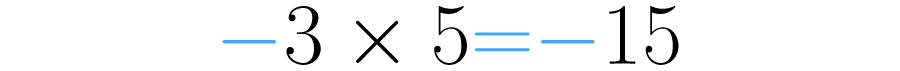
Observa otro ejemplo, la multiplicación . Primero realiza la multiplicación de los números sin tener en cuenta los signos, se tiene que .
Aplicando la ley de signos se encuentra que “menos por menos es más”. Por lo tanto el resultado debe ser un número positivo. Podemos afirmar entonces que .
Ley de los signos para suma
Para ello existen algunas reglas:
- En suma de números positivos con números positivos, el resultado es un número positivo.
- De ser una suma de un número negativo con otro número negativo, el resultado es negativo.
- Si se trata de un número positivo con un número negativo el signo en el resultado es del número entero de mayor valor.
Nota: se debe tomar en cuenta que si un número no posee un signo evidente este se sobre entiende que es de signo positivo + y no es necesario escribirlo. En el caso de ser un resultado negativo, se necesita escribir el signo negativo.
Ejemplos:
Ley de los signos para resta
En este caso la ley aplica en el mismo sentido de la suma, poniéndose en práctica las mismas reglas.
Ley de los signos para multiplicación y división
Para estas operaciones también existen diversas normas muy parecidas a la suma
- En el caso de multiplicar o dividir un signo positivo con otros positivo el resultado es positivo.
- De multiplicar o dividir un signo negativo con otro negativo el resultado será positivo.
- Por último si se multiplica o divide un signo negativo con uno positivo o viceversa siempre será negativos, sin tomar en cuenta el mayor valor del número.
Los signos de agrupación son aquellos que por su origen define cual es el orden en el que se hará una operación. En total son 4 los signos de agrupación, entre los cuales están el paréntesis (), el corchete [], las llaves {} y la barra o vínculo ӀӀ.
La finalidad de esto es realizar un conjunto entre las cantidades de números que se encuentren dentro de los mismos. Lo que quiere decir que un solo conjunto o suma. Se debe conocer muy claramente cuáles son las reglas entre los mismos ya que en una sola operación pueden estar presentes varios signos.
Es decir, si se tiene a + (b-c) esto quiere decir que el primer elemento que esa debe ser sumado a la cantidad que se encuentra dentro del signo de agrupación (). Tomando esto en cuenta significa que dentro del paréntesis o signos de agrupación se le debe conceder un signo a cada elemento bien sea positivo o negativo antes de eliminarlos. En este caso para poder aplicar este proceso se deben aplicar algunas reglas referentes.

Cómo eliminar los signos de agrupación
Dentro de las expresiones algebraicas existen diversas formas para reducir los signos. Pero para ello se deben de poner en práctica algunas reglas, entre las cuales estas:
- En primer lugar se debe mantener el mismo signo para cada elemento dentro de los signos, siempre y cuando vayan antecedidos del signo +.
- En segundo lugar se deben cambiar el signo de los elementos dentro de los signos en el caso de estar antecedidos del signo -.
Los signos grupales se deben eliminar desde adentro hacia afuera, siendo este el orden.
Por otro lado si se encuentra un signo negativo antes del signo de agrupación, se deben eliminar los signos de agrupación y se mantienen los elementos que estaban dentro cambiando solo el signo de cada uno.
Ejemplo
Si el signo de agrupación se encuentra antecedido por un signo positivo. Al igual se deben eliminar los signos de agrupación y mantener los elementos manteniendo todos los signos tal cual.
Los signos de agrupación son utilizados para realizar un conjunto de elementos. Con respecto a estas operaciones dentro del signo de agrupación se realizan primero.
En caso de encontrarse un signo x o multiplicación se debe pasar a multiplicar los elementos que se encuentren dentro de los signos, siempre y cuando se trate de monomios.
Si aparece un signo / o división se realiza el mismo procedimientos que con la multiplicación.
Frecuentemente los paréntesis suelen repetirse dentro de los mismos paréntesis. Tomando en cuenta este caso se utilizan otros signos de agrupación, como por ejemplo [(x+4)+3]. A propósito de esto y para evitar todo tipo de confusión se deben eliminar en primer lugar los signos que están dentro y luego los externos.
Expresiones algebraicas y signos de agrupación
Una expresión algebraica representa un conjunto de elementos entre cantidades numéricas unidas a través de signos de agrupación y ejecutadas a través de signos de operaciones como lo son los signos de suma, resta, multiplicación, división, potencias y raíces. Una expresión algebraica está comprendida entre los siguientes signos como los corchetes, llaves, paréntesis y barras. Así mismo son llamados signos de colección, que tienen el fin de simplificar la operación manteniendo un orden específico.
8x−{2+5x−[6x+(7x−5)−x]}
Cabe destacar que cuando se trata de signos semejantes, es decir, elementos que tengan las mismas letras, la eliminación de estos elementos va a tratar de realizar un elemento de o más elementos similares, sumando o restando sus coeficientes. Pero para reducir estos términos de igual forma se necesitan seguir reglas en todo el procedimiento como lo son:
En primer lugar se deben agrupar los términos semejantes.
Cuando los términos posean los mismos signos, en primer caso se deben sumar los coeficientes y se conserva el mismo signo.
Si resulta tener un signo diferente el elemento mayor se resta al menor, obteniendo así un resultado que debe tener el signo del elemento mayor.
Ejemplo para eliminar signos de agrupación
Como en el próximo ejemplo se va a simplificar la siguiente expresión algebraica, eliminado los signos de agrupación desde el más adentro. Tomando las consideraciones antes mencionadas.
2x – {5+ 3x – [4x + (2x – 5) – x]}
El primer signo que se debe eliminar es el paréntesis, obteniendo la siguiente expresión:
2x – {5 + 3x – [4x + 2x – 5 – x]}
Luego de esto se debe seguir con la reducción de los términos semejantes que se encuentran dentro de los corchetes, logrando lo siguiente:
2x – {5 + 3x – [5x – 5]}
Procedimiento a seguir, eliminar los corchetes
2x – {5 + 3x – 5x +5}
En este punto se deben reducir los términos semejantes que se encuentran dentro de las llaves
2x – {10 – 2x}
Se eliminan las llaves como último paso de eliminación de signos de agrupación
2x – 10 + 2x
Para finalizar se reduce el resultado
4x – 10
Importancia de los signos de agrupación
Ley de los signos matemática, suma, resta, multiplicación y división
Los signos de matematicas conocidos como +, -, x y /, son simbolos aritmeticos para indicar el estado de una operación matemática. Este tipo de operaciones son conocidas como la adicion, sustraccion, multiplicacion y division. Así mismo también pueden englobar a los signos algebraicos en las operaciones.
La matemática es una de las ciencias que estudia todo lo relacionado con los números, figuras geométricas, símbolos y más. Las matemáticas se fueron creando con base a teorías, definiciones y leyes relacionadas entre sí. Es por ello que la mayoría de sus ideas fueron descubiertas de más de 4000 años. El desarrollo constante de la civilización ha sido en gran parte por las matemáticas y otras ciencias que se combinan.
Este tipo de ciencia es aquella que se encarga de descifrar y trabajar con elementos abstractos que estén relacionados entre ellos. Para ser utilizado se necesita el razonamiento lógico. Es por ello que su uso ha sido importante para el desarrollo en avances tecnológicos. Esta se divide en cuatros ramas como lo son la aritmética, álgebras, geometría y estadística. En la actualidad se utilizan las matemáticas como una herramienta para las vida cotidiana.
A pesar que se ha afirmado que en las matemáticas no existen leyes si se puede asegurar que existan normas o condiciones para poder realizar las operaciones sin ningún tipo de problema. En matemáticas existen leyes que se encargan de signos para realizar las operaciones más básicas como lo son suma, resta, división y multiplicación. Este tipo de ley es la que se ocupa del sentido de las operaciones, como se ejercen y la dirección de los signos. Es por ello que a continuación daremos un resumen de la ley de los signos de matemáticas.

Ley de los signos de matemática
Dicha ley de los signos está basada en la multiplicación. Es decir se rige para que los números se multipliquen como corresponda. La ley se basa en lo siguiente: si los signos son iguales el resultado debe ser positivo. En cambio si los signos son diferentes el resultado será negativo. En otras palabras podría decirse signos iguales se suman, signos diferentes se restan. Esto va relacionado en operaciones básicas con números enteros. Es por ello que esta forma o ley se debe memorizar de una forma simple para realizar otro tipo de operaciones.
Como antes se mencionó la ley de los signos va a enfocarse en los signos + y -, que se denomina más o positivo y menos de negativo. En el caso de las operaciones de suma y resta de números enteros el resultado positivo será representado por el signo + y el resultado negativo por el signo –. Sin embargo para la multiplicación y división va a corresponder el positivo si los dos números son positivos y negativo si se encuentra un número positivo y otro negativo. Así mismo se puede observar en operaciones de ecuaciones algebraicas.
En general la ley de los signos está relacionada con el resultado de una operación entre números positivos y negativos. Es decir el resultado entre dos numero positivos será positivo. De igual forma se puede decir que el resultado entre un número positivo y negativo será negativo. Por otro lado dos números negativos tendrán por resultado un número positivo. A continuación representamos una fórmula para la ley de los signos.
(+) . (+)= (+) (el resultado de una operación dos números positivos es positivo)
(-) . (-)= (+) (el resultado de una operación número negativo y uno negativo es positivo)
(+) . (-)= (-) (el resultado de una operación número positivo y uno negativo es negativo)
(-) . (+)= (-) (el resultado de una operación número negativo y uno positivo es negativo)
Ley de los signos para suma
Para ello existen algunas reglas:
- En suma de números positivos con números positivos, el resultado es un número positivo.
- De ser una suma de un número negativo con otro número negativo, el resultado es negativo.
- Si se trata de un número positivo con un número negativo el signo en el resultado es del número entero de mayor valor.
Nota: se debe tomar en cuenta que si un número no posee un signo evidente este se sobre entiende que es de signo positivo + y no es necesario escribirlo. En el caso de ser un resultado negativo, se necesita escribir el signo negativo.
Ejemplos:
4 + 8= 12
(-5) + (-6)= -11
-7 + 4= -3
Ley de los signos para resta
En este caso la ley aplica en el mismo sentido de la suma, poniéndose en práctica las mismas reglas.
(+6) – (+2)= +4
(-7) – (-4)= -3
Ley de los signos para multiplicación y división
Para estas operaciones también existen diversas normas muy parecidas a la suma
- En el caso de multiplicar o dividir un signo positivo con otros positivo el resultado es positivo.
- De multiplicar o dividir un signo negativo con otro negativo el resultado será positivo.
- Por último si se multiplica o divide un signo negativo con uno positivo o viceversa siempre será negativos, sin tomar en cuenta el mayor valor del número.
(+6) ÷ (+4)= +1,5
(-8) ÷ (-4)= +2
(+4) ÷ (-2)= -2
Importancia de la ley de los signos
Como se mencionó anteriormente las matemáticas son realmente importantes como una herramienta para la evolución y creación de nuevos teoremas y más. En nuestra vida cotidiana se utilizan en un sinfín de situaciones como el administrar dinero, calcular distancias, y el razonamiento matemático.
Conocer con exactitud las matemáticas y aprender sus normas y leyes se trata de crear habilidades para resolver problemas importantes en la vida. Las matemáticas y todo lo que las relaciones como lo son sus leyes son relevantes para el desarrollo de un país, la innovación, vanguardia y exigencias económicas. El dominio de las matemáticas es una cuestión que tiene que ver con grandes aspectos de todo el mundo.
Las matemáticas en algunas ocasiones suelen ser un poco difíciles de entender. Sin embargo se debe tomar en cuenta que en el caso de la ley de los signos es una muy sencilla de aplicar y de aprender. Se trata de adquirir y poner en práctica conocimientos importantes que desde siempre son enseñados en cualquier nivel educativo. Es por ello que no se debe dejar a un lado este tipo de aprendizaje y aprovechar todo las clases y teorías relacionadas a las mismas.
Cálculo del máximo común divisor
Hallar el  de:
de:  y
y  .
.
1Descomponemos los números en factores primos

Así, los números se escriben de la forma

2Los factores comunes con menor exponente son 
3Para calcular el  multiplicamos los factores comunes con menor exponente
multiplicamos los factores comunes con menor exponente

Hay que notar que si un número es divisor de otro, entonces éste es el  de ambos
de ambos
Ejemplo: El número  es divisor de
es divisor de  , por lo que
, por lo que 
Mínimo común múltiplo
Hallar el  de:
de:  y
y  .
.
1Descomponemos los números en factores primos

Así, los números se escriben de la forma

2Los factores comunes y no comunes con mayor exponente son 
3Para calcular el  multiplicamos los factores comunes y no comunes con mayor exponente
multiplicamos los factores comunes y no comunes con mayor exponente

Así,  es el menor número que puede ser dividido por
es el menor número que puede ser dividido por  y
y  .
.
Hay que notar que si un número es múltiplo de otro, entonces éste es el  de ambos
de ambos
Ejemplo: El número  es múltplo de
es múltplo de  , por lo que
, por lo que 
Ejercicios propuestos
1Calcular el  y
y  de
de  y
y 
2Calcular el  y
y  de
de  y
y 
3Calcular el  y
y  de
de  y
y 
4Calcular el  y
y  de
de  y
y 
5Calcular el  y
y  de
de  y
y 
1.- Mínimo común múltiplo
Los múltiplos de un número se obtienen multiplicando el número por 1, 2, 3, 4...
Por ejemplo: los múltiplos de 4 son: 4, 8, 12, 16, 20, 24, 28...
El Mínimo Común Múltiplo (MCM) de 2 o más número es el menor de lo múltiplos comunes a estos números:
Por ejemplo: vamos a calcular el MCM de 3 y 4:
Múltiplos de 3: 3, 6, 9, 12, 15, 18, 21, 24...
Múltiplos de 4: 4, 8, 12, 16, 20, 24, 28...
Vemos que 12 es un múltiplo de ambos números y es el menor de los múltiplos comunes. Por lo tanto 12 es el Mínimo Común Múltiplo.
2.- Máximo común divisor
Los divisores de un número son aquellos que al dividir el número el resto es 0.
Por ejemplo: Divisores de 24 son: 1, 2, 3, 4, 6, 12 y 24.
Si se divide 24 por cualquiera de ellos el resto es 0.
El Máximo Común Divisor (MCD) de 2 o más número es el mayor de los divisores comunes a estos números:
Por ejemplo: vamos a calcular el MCD de 30 y 42:
Divisores de 30: 1, 2, 3, 5, 6, 10, 15 y 30.
Divisores de 42: 1, 2, 3, 6, 7, 21 y 42.
Vemos que 6 es un divisor común a ambos números y es el mayor de los divisores comunes. Por lo tanto 6 es el Máximo Común Divisor.
Ejercicios
1. Calcula el MCM :

2. Calcula el MCD :

Máximo común divisor
“El divisor común de dos o más números es todo número que los divide a todos exactamente “
Ejemplo.
12 es divisible por 2, por 3, por 4,por 6, por 12.
24 es divisible por 2, por 3, por 4,por 6, por 12, por 24.
Los divisores comunes de 12 y 24 son: 2, 3, 4, 6 y 12.
“El máximo común divisor de dos o más números es el mayor número que los divide a todos exactamente”
Se designa por las iniciales m.c.d.
El m.c.d de 12 y 24 es 12 (corresponde al divisor común más grande de 12 y 24 ).
Ejemplo: Obtener el m.c.d. de 12 y de 24 por factorización
Se dividen por 2 el 12 y el 24
Escribimos abajo de 12 el cociente 6 y abajo de 24 el cociente 12 (resultado de las divisiones anteriores)
Dividimos ahora el 6 y el 12 por 2 y sus cocientes (3 y 6) se anotan abajo de ellos
Ahora dividimos el 3 por 3 y el 6 por 2 (el 3 no es divisible por 2 exactamente) y sus cocientes 1 y 3 los anotamos abajo del 3 y del 6
Ahora se divide por 3 el 3 y su cociente 1 se pone debajo.
Como los dos números ya tienen como cociente al 1, hemos terminado la Factorización de números
La descomposición en factores primos del 12 es = 2 x 2 x 3 = 2² x 3
La descomposición en factores primos del 24 es = 2 x 2 x 2 x 3 = 2³ x 3
El m.c.d. de 12 y de 24 es el producto de todos los factores primos comunes (que están en los dos números = 2 y 3) afectados por su menor exponente (2² y 2³, el menor es 2²) y el 3 que sólo aparece una vez en cada número.
Por lo tanto el m.c.d. de 12 y de 24 es el producto de 2² x 3 = 12
Métodos para hallar el m.c.d.
Existen tres métodos:
a) Por inspección
b) Por divisiones sucesivas
c) Por Factorización de números
a) Por inspección.
Este método se utiliza cuando los números son pequeños.
Consiste en ver si el menor de los números divide a todos los demás y si los divide, éste será el m.c.d. Si no los divide buscamos los divisores de ese número y escogemos al mayor que los divide a todos. Ése será el m.c.d.
Ejemplo. Obtener el m.c.d. de 12, 24 y 48
El número menor 12,divide a 24 (24 ÷ 12 = 2) y también divide a 48 (48 ÷ 12 = 4) Entonces 12 es el m.c.d. de 12, 24 y 48.
Obtener el m.c.d. de 30, 50 y 60. El número menor 30,divide a 60 (60 ÷ 30 = 2) pero no divide a 50 Buscamos los divisores de 30: 2, 3, 5, 6, 10, 15.
Y escojo al mayor de estos divisores que divide a los tres números. 15 no puede ser porque no divide a 50, En este caso el 10 si divide a 30, 50 y 60.
El máximo común divisor (m.c.d.) de 30,50 y 60 es 10
b) Por divisiones sucesivas.
Este método se utiliza cuando los números son más grandes.
Consiste en dividir el mayor de los números dados por el menor. Si la división es exacta, el número menor es el m.c.d. de los números dados.
Si la división es inexacta, se divide el divisor por el primer residuo, el primer residuo por el segundo residuo, éste por el tercero y así sucesivamente hasta obtener una división exacta. El último divisor será el m.c.d.
Ejemplo. Obtener el m.c.d. de 1284 y 428
Dividimos al número mayor por el menor: 1284 ÷ 428 = 3 La división es exacta.
Entonces 428 es el m.c.d. de 1284 y 428.
Obtener el m.c.d. de 128 y 460
Dividimos 460 ÷ 128 = 3 y sobran 76, es una división inexacta.
Ahora divido 128 que es el divisor, entre 76 que es mi primer residuo: 128 ÷ 76 = 1 y sobran 52.
Divido el divisor 76 entre mi segundo residuo: 76 ÷ 52 = 1 sobran 24.
Divido el divisor 52 entre el tercer residuo 24: 52 ÷ 24 = 2 y sobran 4.
Divido el divisor 24 entre el cuarto residuo 4: 24 ÷ 4 = 6 y llego a una división exacta.
Al llegar a la división exacta 24 ÷ 4 = 6 llego al m.c.d. de 460 y 128, siendo éste el último divisor que es 4.
El máximo común divisor (m.c.d.) de 128 y 460 es 4
Si al hallar el m.c.d. encontramos un residuo que sea primo y la división siguiente no es exacta, ya no se continua dividiendo y el m.c.d. es 1; porque los números son primos entre sí.
c) Por descomposición en factores primos (Factorización de números).
El m.c.d. de varios números descompuestos en factores primos, es el producto de sus factores primos comunes afectados de su menor exponente.
Es decir que los números dados se descomponen en sus factores primos por medio de la factorización, de estos factores primos se escogen los que son comunes a los números; y de éstos se toman los que tengan el menor exponente(que se repiten menos veces).
Ejemplo. Obtener el m.c.d. de 170 y 204
Se dividen por 2 el 170 y el 204
Escribimos abajo de 170 el cociente 85 y abajo de 204 el cociente 102 (resultado de las divisiones anteriores)
Dividimos ahora el 85 ÷ 5 (porque no es divisible por los factores primos 2 y 3) y el 102 ÷ 2 y sus cocientes (17 y 51) se anotan abajo de ellos
Ahora dividimos el 17 ÷ 17 (porque es número primo y sólo se divide por sí mismo y por la unidad) y el 51 ÷ 3 (ya que no es divisible por 2 exactamente) y sus cocientes 1 y 17 los anotamos abajo del 17 y del 51
Ahora se divide por 17 el 17 y su cociente 1 se pone debajo.
Como los dos números ya tienen como cociente al 1, hemos terminado de factorizarlos.
La descomposición en factores primos del 170 es = 2 x 5 x 17
La descomposición en factores primos del 204 es = 2 x 2 x 3 x 17 = 2² x 3 x 17
El m.c.d. de 170 y 204 es el producto de todos los factores primos comunes (que están en los dos números = 2 y 17)afectados por su menor exponente (de 2 y 2², el menor es 2) y el 17 que sólo aparece una vez en cada número.
Por lo tanto el m.c.d. de 170 y de 204 es el producto de 2 por 17 = 34
Método abreviado
Para hallar el m.c.d. de varios números por descomposición en factores primos (Factorización de números), se dividen al mismo tiempo todos los números dados por un factor común, los cocientes nuevamente por un factor común y así sucesivamente.
El m.c.d. es el producto de los factores primos.
Ejemplo: Obtener el m.c.d. de 48, 36 y 84 .
Ejemplos de problemas donde puedo utilizar el m.c.d.
Algunos problemas que puedo resolver con el m.c.d. son los siguientes:
1.- Dos cintas de 36 metros y 48 metros de longitud se quieren dividir en pedazos iguales y de la mayor longitud posible. ¿Cuál será la longitud de cada pedazo?
2.- Se tienen tres varillas de 60 cm, 80 cm, y 100 cm de longitud respectivamente. Se quieren dividir en pedazos de la misma longitud sin que sobre nada. Menciona tres longitudes posibles para cada pedazo.
3.- Si tengo 80 chocolates para guardar en cajas, ¿qué cantidades puedo poner en cada caja sin que sobren chocolates y cuántas cajas necesito?
Se divide cada uno de los números dados por su menor divisor; lo mismo se hace con los cocientes hasta obtener que todos los cocientes sean 1. El mcm sera el producto de todos los divisores primos.
Si un número no es divisible por un factor primo se repite debajo (se baja) como sigue en los ejemplos siguientes.
1.- Hallar el MCD de 160, 210 y 100.
| 160 | 210 | 100 | 2 |
| 80 | 105 | 50 | 2 |
| 40 | 105 | 25 | 2 |
| 20 | 105 | 25 | 2 |
| 10 | 105 | 25 | 2 |
| 5 | 105 | 25 | 3 |
| 5 | 35 | 25 | 5 |
| 1 | 7 | 5 | 5 |
| 7 | 1 | 7 | |
| 1 |
El M.C.D. es 2x5 =10
Máximo común divisor
“El divisor común de dos o más números es todo número que los divide a todos exactamente “
Ejemplo.
12 es divisible por 2, por 3, por 4,por 6, por 12.
24 es divisible por 2, por 3, por 4,por 6, por 12, por 24.
Los divisores comunes de 12 y 24 son: 2, 3, 4, 6 y 12.
“El máximo común divisor de dos o más números es el mayor número que los divide a todos exactamente”
Se designa por las iniciales m.c.d.
El m.c.d de 12 y 24 es 12 (corresponde al divisor común más grande de 12 y 24 ).
Ejemplo: Obtener el m.c.d. de 12 y de 24 por factorización
Se dividen por 2 el 12 y el 24
Escribimos abajo de 12 el cociente 6 y abajo de 24 el cociente 12 (resultado de las divisiones anteriores)
Dividimos ahora el 6 y el 12 por 2 y sus cocientes (3 y 6) se anotan abajo de ellos
Ahora dividimos el 3 por 3 y el 6 por 2 (el 3 no es divisible por 2 exactamente) y sus cocientes 1 y 3 los anotamos abajo del 3 y del 6
Ahora se divide por 3 el 3 y su cociente 1 se pone debajo.
Como los dos números ya tienen como cociente al 1, hemos terminado la Factorización de números
La descomposición en factores primos del 12 es = 2 x 2 x 3 = 2² x 3
La descomposición en factores primos del 24 es = 2 x 2 x 2 x 3 = 2³ x 3
El m.c.d. de 12 y de 24 es el producto de todos los factores primos comunes (que están en los dos números = 2 y 3) afectados por su menor exponente (2² y 2³, el menor es 2²) y el 3 que sólo aparece una vez en cada número.
Por lo tanto el m.c.d. de 12 y de 24 es el producto de 2² x 3 = 12
Métodos para hallar el m.c.d.
Existen tres métodos:
a) Por inspección
b) Por divisiones sucesivas
c) Por Factorización de números
a) Por inspección.
Este método se utiliza cuando los números son pequeños.
Consiste en ver si el menor de los números divide a todos los demás y si los divide, éste será el m.c.d. Si no los divide buscamos los divisores de ese número y escogemos al mayor que los divide a todos. Ése será el m.c.d.
Ejemplo. Obtener el m.c.d. de 12, 24 y 48
El número menor 12,divide a 24 (24 ÷ 12 = 2) y también divide a 48 (48 ÷ 12 = 4) Entonces 12 es el m.c.d. de 12, 24 y 48.
Obtener el m.c.d. de 30, 50 y 60. El número menor 30,divide a 60 (60 ÷ 30 = 2) pero no divide a 50 Buscamos los divisores de 30: 2, 3, 5, 6, 10, 15.
Y escojo al mayor de estos divisores que divide a los tres números. 15 no puede ser porque no divide a 50, En este caso el 10 si divide a 30, 50 y 60.
El máximo común divisor (m.c.d.) de 30,50 y 60 es 10
b) Por divisiones sucesivas.
Este método se utiliza cuando los números son más grandes.
Consiste en dividir el mayor de los números dados por el menor. Si la división es exacta, el número menor es el m.c.d. de los números dados.
Si la división es inexacta, se divide el divisor por el primer residuo, el primer residuo por el segundo residuo, éste por el tercero y así sucesivamente hasta obtener una división exacta. El último divisor será el m.c.d.
Ejemplo. Obtener el m.c.d. de 1284 y 428
Dividimos al número mayor por el menor: 1284 ÷ 428 = 3 La división es exacta.
Entonces 428 es el m.c.d. de 1284 y 428.
Obtener el m.c.d. de 128 y 460
Dividimos 460 ÷ 128 = 3 y sobran 76, es una división inexacta.
Ahora divido 128 que es el divisor, entre 76 que es mi primer residuo: 128 ÷ 76 = 1 y sobran 52.
Divido el divisor 76 entre mi segundo residuo: 76 ÷ 52 = 1 sobran 24.
Divido el divisor 52 entre el tercer residuo 24: 52 ÷ 24 = 2 y sobran 4.
Divido el divisor 24 entre el cuarto residuo 4: 24 ÷ 4 = 6 y llego a una división exacta.
Al llegar a la división exacta 24 ÷ 4 = 6 llego al m.c.d. de 460 y 128, siendo éste el último divisor que es 4.
El máximo común divisor (m.c.d.) de 128 y 460 es 4
Si al hallar el m.c.d. encontramos un residuo que sea primo y la división siguiente no es exacta, ya no se continua dividiendo y el m.c.d. es 1; porque los números son primos entre sí.
c) Por descomposición en factores primos (Factorización de números).
El m.c.d. de varios números descompuestos en factores primos, es el producto de sus factores primos comunes afectados de su menor exponente.
Es decir que los números dados se descomponen en sus factores primos por medio de la factorización, de estos factores primos se escogen los que son comunes a los números; y de éstos se toman los que tengan el menor exponente(que se repiten menos veces).
Ejemplo. Obtener el m.c.d. de 170 y 204
Se dividen por 2 el 170 y el 204
Escribimos abajo de 170 el cociente 85 y abajo de 204 el cociente 102 (resultado de las divisiones anteriores)
Dividimos ahora el 85 ÷ 5 (porque no es divisible por los factores primos 2 y 3) y el 102 ÷ 2 y sus cocientes (17 y 51) se anotan abajo de ellos
Ahora dividimos el 17 ÷ 17 (porque es número primo y sólo se divide por sí mismo y por la unidad) y el 51 ÷ 3 (ya que no es divisible por 2 exactamente) y sus cocientes 1 y 17 los anotamos abajo del 17 y del 51
Ahora se divide por 17 el 17 y su cociente 1 se pone debajo.
Como los dos números ya tienen como cociente al 1, hemos terminado de factorizarlos.
La descomposición en factores primos del 170 es = 2 x 5 x 17
La descomposición en factores primos del 204 es = 2 x 2 x 3 x 17 = 2² x 3 x 17
El m.c.d. de 170 y 204 es el producto de todos los factores primos comunes (que están en los dos números = 2 y 17)afectados por su menor exponente (de 2 y 2², el menor es 2) y el 17 que sólo aparece una vez en cada número.
Por lo tanto el m.c.d. de 170 y de 204 es el producto de 2 por 17 = 34
Método abreviado
Para hallar el m.c.d. de varios números por descomposición en factores primos (Factorización de números), se dividen al mismo tiempo todos los números dados por un factor común, los cocientes nuevamente por un factor común y así sucesivamente.
El m.c.d. es el producto de los factores primos.
Ejemplo: Obtener el m.c.d. de 48, 36 y 84 .
Ejemplos de problemas donde puedo utilizar el m.c.d.
Algunos problemas que puedo resolver con el m.c.d. son los siguientes:
1.- Dos cintas de 36 metros y 48 metros de longitud se quieren dividir en pedazos iguales y de la mayor longitud posible. ¿Cuál será la longitud de cada pedazo?
2.- Se tienen tres varillas de 60 cm, 80 cm, y 100 cm de longitud respectivamente. Se quieren dividir en pedazos de la misma longitud sin que sobre nada. Menciona tres longitudes posibles para cada pedazo.
3.- Si tengo 80 chocolates para guardar en cajas, ¿qué cantidades puedo poner en cada caja sin que sobren chocolates y cuántas cajas necesito?
Se divide cada uno de los números dados por su menor divisor; lo mismo se hace con los cocientes hasta obtener que todos los cocientes sean 1. El mcm sera el producto de todos los divisores primos.
Si un número no es divisible por un factor primo se repite debajo (se baja) como sigue en los ejemplos siguientes.
1.- Hallar el MCD de 160, 210 y 100.
| 160 | 210 | 100 | 2 |
| 80 | 105 | 50 | 2 |
| 40 | 105 | 25 | 2 |
| 20 | 105 | 25 | 2 |
| 10 | 105 | 25 | 2 |
| 5 | 105 | 25 | 3 |
| 5 | 35 | 25 | 5 |
| 1 | 7 | 5 | 5 |
| 7 | 1 | 7 | |
| 1 |
El M.C.D. es 2x5 =10
¿Qué es el mínimo común múltiplo (mcm)?
El mínimo común múltiplo (mcm) es el número positivo más pequeño que es múltiplo de dos o más números.
Para entender mejor esta definición vamos a ver todos los términos.
Múltiplo
Los múltiplos de un número son los que obtienes cuando lo multiplicas por otros números.
Vamos a ver un ejemplo de los múltiplos de 2 y de 3. Para calcular sus múltiplos hay que ir multiplicando el 2 y el 3 por 1, por 2, por 3, etc.
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
y así sucesivamente hasta infinitos números.
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
y así sucesivamente hasta infinitos números.

Múltiplo Común
Un múltiplo común es un número que es múltiplo a la vez de dos o más números, es decir, es un múltiplo común a esos números.
Siguiendo con el ejemplo anterior, vamos a ver los múltiplos comunes de 2 y de 3.

Habrá que ver qué múltiplos tienen en común el dos y el tres, que en la imagen figuran en verde, es decir, el 6, el 12 y el 18. Hay que tener en cuenta que los múltiplos son infinitos y que nosotros solo hemos mostrados los primeros de cada número.
Mínimo común múltiplo
El mínimo común múltiplo es el número más pequeño de los múltiplos comunes.
Siguiendo con el ejemplo anterior, si los múltiplos comunes de 2 y de 3 eran 6, 12 y 18, el mínimo común múltiplo o mcm es 6, ya que es el menor de los múltiplos comunes.
Cómo calcular el mínimo común múltiplo
Se pueden utilizar dos métodos.
- El primer método para calcular el mcm es el que hemos utilizado antes, es decir, escribimos los primeros múltiplos de cada número, señalamos los múltiplos que sean comunes y elegimos el múltiplo común más pequeño.
- Ahora vamos a explicar el segundo método para calcular el mcm. Lo primero que hay que hacer es descomponer en factores primos cada número. Después tendremos que elegir los factores comunes y no comunes elevados al mayor exponente y por último, tendremos que multiplicar los factores elegidos.
Vamos a ver un ejemplo de ésto, calculando el mcm de 12 y de 8.
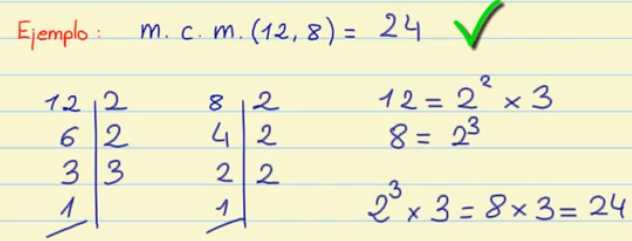
Vamos a descomponer 12 y 8 en factores primos:
12 = 22 x 3
8 = 23
Ahora elegimos los factores comunes y no comunes elevados al mayor exponente, por lo tanto elegimos 23 y el 3.
Y por último los multiplicamos, por lo tanto 23 x 3 = 8 x 3 = 24
Así que el mcm ( 12 , 8 ) = 24
¿Qué es el mínimo común múltiplo (mcm)?
El mínimo común múltiplo (mcm) es el número positivo más pequeño que es múltiplo de dos o más números.
Para entender mejor esta definición vamos a ver todos los términos.
Múltiplo
Los múltiplos de un número son los que obtienes cuando lo multiplicas por otros números.
Vamos a ver un ejemplo de los múltiplos de 2 y de 3. Para calcular sus múltiplos hay que ir multiplicando el 2 y el 3 por 1, por 2, por 3, etc.
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
y así sucesivamente hasta infinitos números.
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
y así sucesivamente hasta infinitos números.

Múltiplo Común
Un múltiplo común es un número que es múltiplo a la vez de dos o más números, es decir, es un múltiplo común a esos números.
Siguiendo con el ejemplo anterior, vamos a ver los múltiplos comunes de 2 y de 3.

Habrá que ver qué múltiplos tienen en común el dos y el tres, que en la imagen figuran en verde, es decir, el 6, el 12 y el 18. Hay que tener en cuenta que los múltiplos son infinitos y que nosotros solo hemos mostrados los primeros de cada número.
Mínimo común múltiplo
El mínimo común múltiplo es el número más pequeño de los múltiplos comunes.
Siguiendo con el ejemplo anterior, si los múltiplos comunes de 2 y de 3 eran 6, 12 y 18, el mínimo común múltiplo o mcm es 6, ya que es el menor de los múltiplos comunes.
Cómo calcular el mínimo común múltiplo
Se pueden utilizar dos métodos.
- El primer método para calcular el mcm es el que hemos utilizado antes, es decir, escribimos los primeros múltiplos de cada número, señalamos los múltiplos que sean comunes y elegimos el múltiplo común más pequeño.
- Ahora vamos a explicar el segundo método para calcular el mcm. Lo primero que hay que hacer es descomponer en factores primos cada número. Después tendremos que elegir los factores comunes y no comunes elevados al mayor exponente y por último, tendremos que multiplicar los factores elegidos.
Vamos a ver un ejemplo de ésto, calculando el mcm de 12 y de 8.
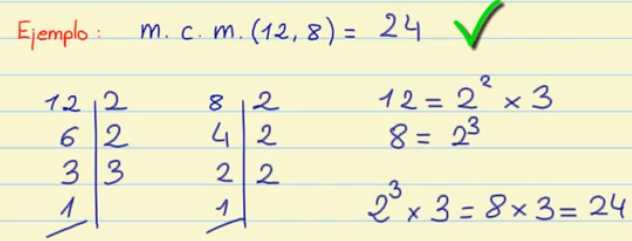
Vamos a descomponer 12 y 8 en factores primos:
12 = 22 x 3
8 = 23
Ahora elegimos los factores comunes y no comunes elevados al mayor exponente, por lo tanto elegimos 23 y el 3.
Y por último los multiplicamos, por lo tanto 23 x 3 = 8 x 3 = 24
Así que el mcm ( 12 , 8 ) = 24
a palabra factor: un término que está multiplicando. Por ejemplo, en la expresión , cuatro es factor de cinco, y cinco es factor de cuatro, ya que cada uno está multiplicando al otro. ¿Nada más sencillo verdad? Ahora podrás comprender más profundamente que significa factorizar un número.
Es posible representar veinte unidades, por ejemplo, de varias formas: , ó son algunas de ellas. Pero ¿se puede escribir en factores? Es decir, ¿se puede escribir veinte representado como una multiplicación de números enteros? Claro: , por lo tanto se dice que es una factorización de . Factorizar un número es encontrar una forma de escribirlo como multiplicación. Observa que los factores son precisamente divisores del número.
Esto tiene sentido solo para números compuestos, pues para los números primos la descomposición es trivial. Por ejemplo, las únicas factorizaciones posibles de son: y .
Como te podrás imaginar, se puede factorizar (o descomponer) un número de muchas formas distintas.
Tomemos como ejemplo el número . En la siguiente imagen puedes observar algunas de las formas en las que es posible descomponerlo.
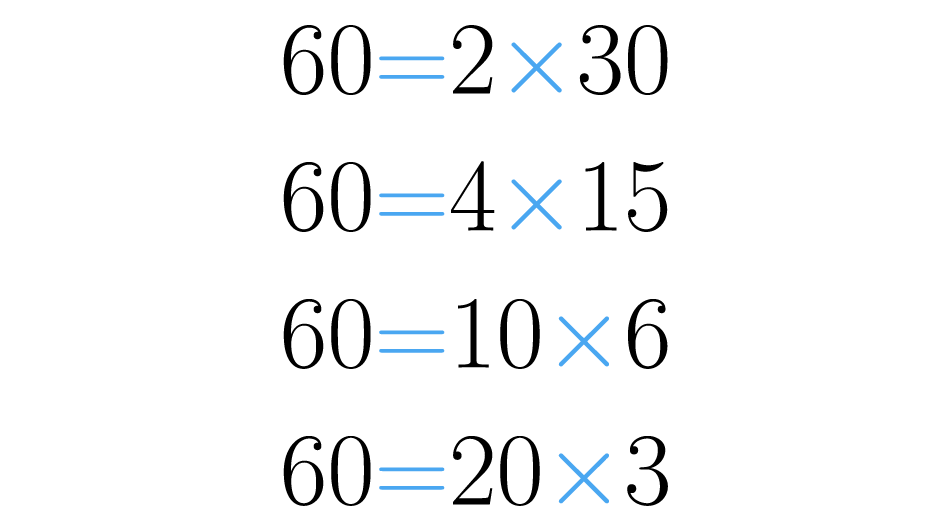
Una forma única gracias a los primos
Recuerda que los números primos son aquellos mayores que uno, que tienen solo dos divisores: uno y ellos mismos. Los demás números, los compuestos, tienen varios divisores. Por esta razón siempre podremos descomponer los números hasta que cada uno de sus factores sea primo. Observa:
Tomemos una de las factorizaciones del número , por ejemplo . Observa que seis y diez son números compuestos, pues y .
Lo anterior quiere decir que se pueden descomponer seis y diez en más factores, por ejemplo: y . Por lo tanto la descomposición de se transforma así:
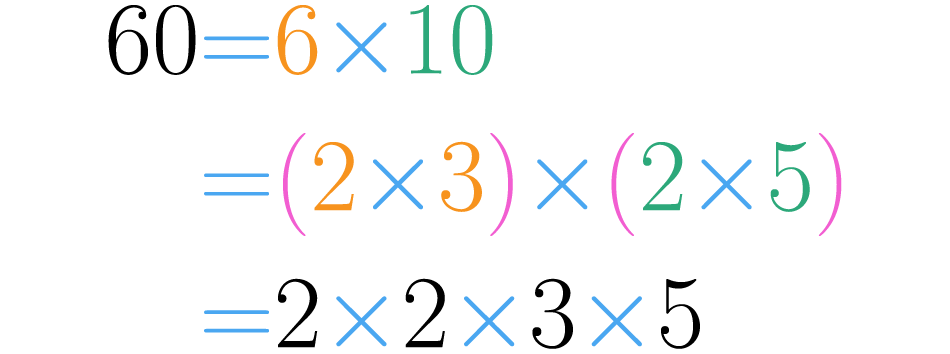
Usando las propiedades conmutativa y asociativa de la multiplicación, podemos escribir la descomposición de menor a mayor y sin paréntesis, como lo indica la última igualdad de la imagen anterior.
Ahora cada uno de los factores en la descomposición de es un número primo, y como estos no tienen más divisores que uno y ellos mismos, no es posible seguir transformándola, salvo por el orden.
Fíjate en que si se hubiera comenzado por otra descomposición de , se llegaría al mismo resultado.
Observa que la única diferencia entre esta descomposición y la obtenida anteriormente, es el orden de los factores primos.
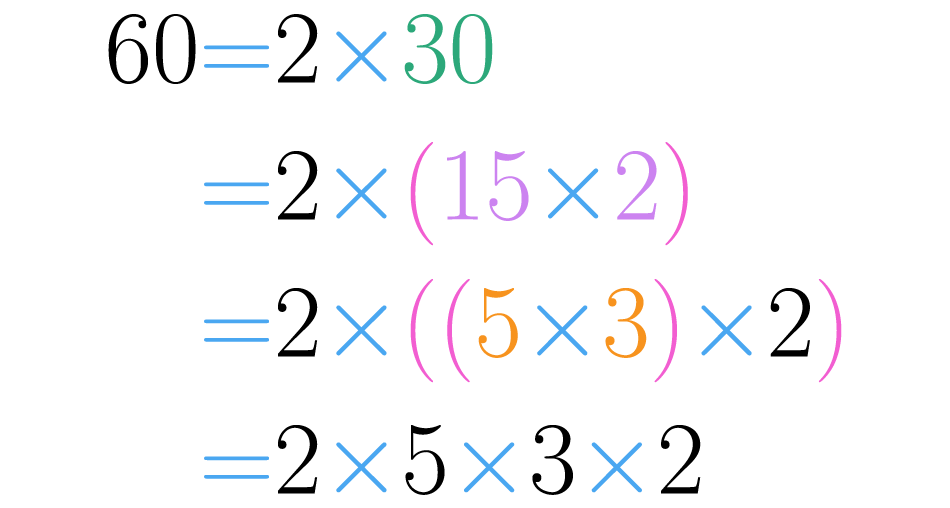
Lo anterior vale para todos los números, y significa que todo número natural mayor que uno, o es primo, o se puede escribir como producto de primos. Esta afirmación es una de las más importantes de la matemática, y como tal recibe un nombre especial: teorema fundamental de la aritmética.
Simplificando la notación
A la hora de descomponer números en factores primos se pueden encontrar algunos con una gran cantidad de factores. Un ejemplo de ello es :
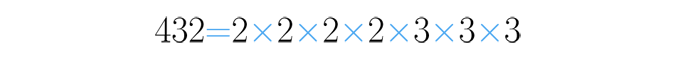
Para simplificar la escritura de estas descomposiciones se hace lo siguiente: solo anotamos una vez cada factor primo, pero escribimos las veces que se repite con un pequeño número arriba al lado derecho.
Así, la descomposición de se expresa: , ya que el factor dos aparece cuatro veces y el factor tres aparece tres. Leemos este tipo de expresiones así: “dos a la cuatro, por tres a la tres”.
En la expresión se conoce a como exponente, mientras que es llamado base. En la expresión , es el exponente y es la base. A esta forma de escribir los productos se le conoce como potenciación.
Descomposición de un número en factores primos
Todo número compuesto se puede escribir como multiplicación de dos o más factores primos.
Para descomponer un número en producto de factores primos se siguen estos pasos:
1° Se escribe el número a la izquierda de una raya vertical (actúa como "ventana" de división) y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto.
2° Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.
Ejemplo 1: Realiza la descomposición en producto de factores primos del número 24:
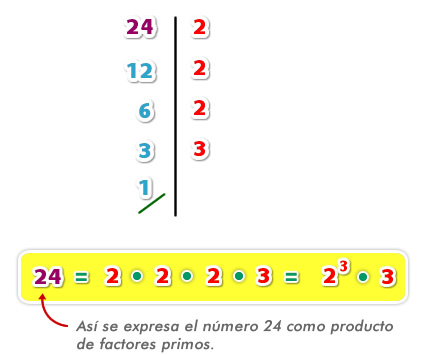
Los números que están a la izquierda de la línea, son los cocientes parciales y los de la derecha, son los factores primos.
Recuerda que siempre debes comenzar por el menor número primo por el cual, el número que te están preguntando, sea divisible.
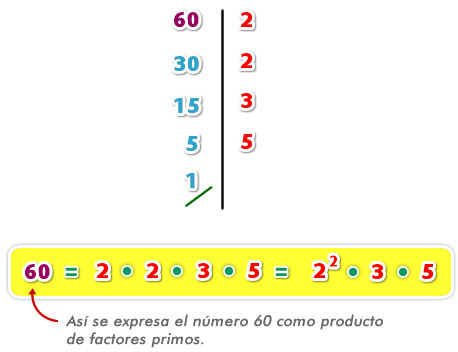
Ejemplo 2: Realiza la descomposición en producto de factores primos del número 60:
Criterio de divisibilidad del 9
Un número es divisible entre 9 si la suma de sus cifras es múltiplo de 9.
Nota: Si el número tiene cifras que sean 9, si se quiere, no es necesario sumar dichas cifras (las cifras que son 9). De esa manera, como la suma total de cifras es menor, es más fácil ver si es múltiplo de 9.
Por ejemplo:
1845 es divisible entre 9, porque 1+8+4+5=18, y 18 es múltiplo de 9 (18=9·2).
39744 es divisible entre 3, porque 3+7+4+4=18 (el 9 no lo hemos sumado), y 18 es múltiplo de 9 (18=9·2).
5408 no es divisible entre 9, porque 5+4+0+8=17, y 17 no es múltiplo de 9.
Criterio de divisibilidad del 10
Un número es divisible entre 10 si termina en 0.
Por ejemplo:
340 es divisible entre 10, porque termina en 0.
23480 es divisible entre 10, porque termina en 0.
239 no es divisible entre 10, porque no termina en 0.
Criterio de divisibilidad del 25
Un número es divisible entre 25 si sus dos últimas cifras son 00, o un múltiplo de 25 (25, 50 ó 75).
Por ejemplo:
750 es divisible entre 25 porque termina en 50, que es múltiplo de 25 (50=25·2).
2375 es divisible entre 25 porque termina en 75, que es múltiplo de 25 (75=25·3).
600 es divisible entre 25 porque termina en 00.
Criterio de divisibilidad del 100
Un número es divisible entre 100 si termina en 00.
Por ejemplo:
300 es divisible entre 100, porque termina en 00.
5600 es divisible entre 100, porque termina en 00.
2390 no es divisible entre 100, porque no termina en 00.
Criterios de divisibilidad
Los criterios de divisibilidad son reglas para saber si un número es divisible por otro sin necesidad de realizar la división.
Aunque pueden buscarse criterios para todos los números, me dispondré a exponer los más comunes y adaptados al tercer ciclo de Educación Primaria.
Al finalizar la explicación, os mostraré una sencilla imagen explicativa sobre todo lo expuesto a continuación.
- Criterio de divisibilidad por 2: Un número es divisible por 2 si acaba en cifra par o en 0. Ejemplos: 0, 2, 4, 36, 94, 72, ..
- Criterio de divisibilidad por 3: Un número es divisible por 3 si la suma de sus cifras da como resultado un múltiplo de 3. Ejemplos: 3, 13, 33, 54, 72, ..
- Criterio de divisibilidad por 4: Un número es divisible por 4 si sus dos últimos dígitos forman un múltiplo de 4 o el número termina en 00. Ejemplos: 1704, 516, 400, 54748, ..
- Criterio de divisibilidad por 5: Un número es divisible por 5 si su última cifra es 5 o es 0. Ejemplos: 25, 40, 75, 90, ..
- Criterio de divisibilidad por 6: Un número es divisible por 6 si, a su vez, lo es por 2 y 3. Ejemplos: 912.
- Criterio de divisibilidad por 8: Un número es divisible por 8 si sus 3 últimos dígitos forman un múltiplo de 8 o en número termina en 000. Ejemplos: 2888, 15000, ..
- Criterio de divisibilidad por 9: Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9. Ejemplos: 9, 495, 945, ..
- Criterio de divisibilidad por 10: Un número es divisible por 10 si termina en 0. Ejemplos: 20, 50, 200, 6000000, .. (Queda explicada aunque no venga reflejada en la imagen)
- Criterio de divisibilidad por 11: Para saber si un número es divisible por 11 debemos llevar a cabo el siguiente procedimiento:
Sumamos las cifras que ocupan lugares pares, sumamos las cifras que ocupan lugares impares. A la suma mayor le restamos la suma menor, si la diferencia es 0, 11 o múltiplo de 11 entonces el número es múltiplo de 11, por lo que podrás ser divisible por éste.
(No aparece en la imagen pero he creído conveniente explicarlo y que quede reflejado también).
Múltiplos
Múltiplos de un número Los múltiplos de un número se obtienen multiplicando ese número por los números naturales.
- Son múltiplos de 2 los números 0, 2, 4, 6, 8, 10,12, 14... y muchos más.
- Se obtienen al multiplicar 2x0, 2x1, 2x2, 2x3, etc.
- Escribimos así los múltiplos de 2. → m (2) = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.... }

- Son múltiplos de 3 los números 0, 3, 6, 9, 12, 15, 18, 21...
- Se obtienen al multiplicar 3x0, 3x1, 3x2, 3x3, etc.
- Lo escribimos así → m (3) = {0, 3, 6, 9, 12, 15, 18, 21,.... }
¡OBSERVA!
Los múltiplos de un número son infinitos, como infinitos son los números naturales.
Un múltiplo siempre es un número mayor
El número 0 es múltiplo de todos los números (porque al multiplicar cualquier número por cero siempre nos da cero de resultado)... es algo extraño, pero así son las cosas relacionadas con el número 0.
Los múltiplos de un número se obtienen multiplicando ese número por los números naturales.
- Son múltiplos de 2 los números 0, 2, 4, 6, 8, 10,12, 14... y muchos más.
- Se obtienen al multiplicar 2x0, 2x1, 2x2, 2x3, etc.
- Escribimos así los múltiplos de 2. → m (2) = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.... }
- Son múltiplos de 3 los números 0, 3, 6, 9, 12, 15, 18, 21...
- Se obtienen al multiplicar 3x0, 3x1, 3x2, 3x3, etc.
- Lo escribimos así → m (3) = {0, 3, 6, 9, 12, 15, 18, 21,.... }
¡OBSERVA!
Los múltiplos de un número son infinitos, como infinitos son los números naturales.
Un múltiplo siempre es un número mayor
El número 0 es múltiplo de todos los números (porque al multiplicar cualquier número por cero siempre nos da cero de resultado)... es algo extraño, pero así son las cosas relacionadas con el número 0.
Divisores
Calcular los divisores de un número
Los divisores de un número natural son los números que lo pueden dividir en una división exacta.
- 3 es divisor de 12 porque 12 : 3 = 4 es una división exacta.
- 5 es divisor de 20 porque 20 : 5 = 4 también es una división exacta.
Ser divisor es justamente lo inverso a ser múltiplo.
- Si 3 es divisor de 12, entonces 12 es múltiplo de 3.
- Si 5 es divisor de 20, entonces 20 es múltiplo de 5.

Algunos ejemplos más:
- Son divisores de 8 los números 1, 2, 4 y 8. Lo escribimos: d (8) = {1, 2, 4 y 8}
- Son divisores de 35 los números 1, 5, 7, 35, es decir: d (35) = {1, 5, 7, 35}
- d (66) = {1, 2, 3, 6, 11, 22, 33, 66}
- d (13) = {1 y 13}
Los divisores de un número natural son los números que lo pueden dividir en una división exacta.
- 3 es divisor de 12 porque 12 : 3 = 4 es una división exacta.
- 5 es divisor de 20 porque 20 : 5 = 4 también es una división exacta.
Ser divisor es justamente lo inverso a ser múltiplo.
- Si 3 es divisor de 12, entonces 12 es múltiplo de 3.
- Si 5 es divisor de 20, entonces 20 es múltiplo de 5.
Algunos ejemplos más:
- Son divisores de 8 los números 1, 2, 4 y 8. Lo escribimos: d (8) = {1, 2, 4 y 8}
- Son divisores de 35 los números 1, 5, 7, 35, es decir: d (35) = {1, 5, 7, 35}
- d (66) = {1, 2, 3, 6, 11, 22, 33, 66}
- d (13) = {1 y 13}
Reflexión
Todo número tiene al menos dos divisores:
- El número 1, porque el uno es divisor de todos los números.
- Él mismo, porque cualquier número es divisor de sí mismo.
Todo número tiene al menos dos divisores:
- El número 1, porque el uno es divisor de todos los números.
- Él mismo, porque cualquier número es divisor de sí mismo.
Criterios de divisibilidad
Los criterios de divisibilidad son reglas para saber si un número es divisible por otro sin necesidad de realizar la división.
Aunque pueden buscarse criterios para todos los números, me dispondré a exponer los más comunes y adaptados al tercer ciclo de Educación Primaria.
Al finalizar la explicación, os mostraré una sencilla imagen explicativa sobre todo lo expuesto a continuación.
- Criterio de divisibilidad por 2: Un número es divisible por 2 si acaba en cifra par o en 0. Ejemplos: 0, 2, 4, 36, 94, 72, ..
- Criterio de divisibilidad por 3: Un número es divisible por 3 si la suma de sus cifras da como resultado un múltiplo de 3. Ejemplos: 3, 13, 33, 54, 72, ..
- Criterio de divisibilidad por 4: Un número es divisible por 4 si sus dos últimos dígitos forman un múltiplo de 4 o el número termina en 00. Ejemplos: 1704, 516, 400, 54748, ..
- Criterio de divisibilidad por 5: Un número es divisible por 5 si su última cifra es 5 o es 0. Ejemplos: 25, 40, 75, 90, ..
- Criterio de divisibilidad por 6: Un número es divisible por 6 si, a su vez, lo es por 2 y 3. Ejemplos: 912.
- Criterio de divisibilidad por 8: Un número es divisible por 8 si sus 3 últimos dígitos forman un múltiplo de 8 o en número termina en 000. Ejemplos: 2888, 15000, ..
- Criterio de divisibilidad por 9: Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9. Ejemplos: 9, 495, 945, ..
- Criterio de divisibilidad por 10: Un número es divisible por 10 si termina en 0. Ejemplos: 20, 50, 200, 6000000, .. (Queda explicada aunque no venga reflejada en la imagen)
- Criterio de divisibilidad por 11: Para saber si un número es divisible por 11 debemos llevar a cabo el siguiente procedimiento:
Sumamos las cifras que ocupan lugares pares, sumamos las cifras que ocupan lugares impares. A la suma mayor le restamos la suma menor, si la diferencia es 0, 11 o múltiplo de 11 entonces el número es múltiplo de 11, por lo que podrás ser divisible por éste.
(No aparece en la imagen pero he creído conveniente explicarlo y que quede reflejado también).
POTENCIACIÓN DE NÚMEROS RACIONALES
Propiedades de potencias de racionales
1 Potencia de un número racional
En una fracción elevado a un exponente, este último se distribuye como exponente del numerador y denominador.

Ejemplo:

2 Potencia de exponente negativo
Un número racional elevado a un exponente negativo se intercambian numerador con denominador y el exponente cambia de signo.


3 Potencia de -1
Un número racional elevado al exponente -1, se intercambian numerador con denominador

Ejemplo:

Leyes de los exponentes en racionales
Las leyes de los exponentes se aplican para todos los números reales, por lo tanto, también son ciertas para los racionales.
Un número racional elevado a 0 es igual a la unidad.

Un número racional elevado a 1 es igual a sí mismo.

3.1 Potencias con la misma base
Es otra potencia con la misma base y cuyo exponente es la suma de los exponentes.

Ejemplo:

3.2 Potencias con el mismo exponente
Es otra potencia con el mismo exponente y cuya base es el producto de las bases.

Ejemplo:

4.1 Potencias con la misma base
Es otra potencia con la misma base y cuyo exponente es la diferencia de los exponentes.

Ejemplo:

4.2 Potencias con el mismo exponente
Es otra potencia con el mismo exponente y cuya base es el cociente de las bases.

Ejemplo:

Es otra potencia con la misma base y cuyo exponente es el producto de los exponentes.
![Rendered by QuickLaTeX.com \displaystyle\left[\left(\frac{a}{b}\right)^n\right]^m =\left(\frac{a}{b}\right)^{n\cdot m}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-3ee79d6a941bb925d9e3e87f0d3cd552_l3.png)
Ejemplo:
![Rendered by QuickLaTeX.com \displaystyle\left[\left(\frac{1}{3}\right)^3\right]^2 =\left(\frac{1}{2}\right)^{6}=\frac{1^{6}}{2^{6}}=\frac{1}{64}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-9bce9799469f251f862f8fe23be4d137_l3.png)
POTENCIACIÓN DE NÚMEROS RACIONALES
Multiplicación
División
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Multiplicación
División
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Multiplicación
División
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Multiplicación
División
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
SEMANA 01 AL 05 DE JUNIO
Multiplicación
División
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Números Decimales
¿Qué son números decimales?

Clasificación de los números decimales
Composición de un número decimal
Operaciones con números decimales
Suma y resta
Multiplicación
División
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Números con signo
|
|
|
La recta numérica
Ley de los signos para suma
- En suma de números positivos con números positivos, el resultado es un número positivo.
- De ser una suma de un número negativo con otro número negativo, el resultado es negativo.
- Si se trata de un número positivo con un número negativo el signo en el resultado es del número entero de mayor valor.
(-5) + (-6)= -11
-7 + 4= -3
Ley de los signos para resta
(-7) – (-4)= -3
Ley de los signos para multiplicación y división
- En el caso de multiplicar o dividir un signo positivo con otros positivo el resultado es positivo.
- De multiplicar o dividir un signo negativo con otro negativo el resultado será positivo.
- Por último si se multiplica o divide un signo negativo con uno positivo o viceversa siempre será negativos, sin tomar en cuenta el mayor valor del número.
(-8) ÷ (-4)= +2
(+4) ÷ (-2)= -2
|
- Representación de fracciones mediante recta numérica
- Directamente
- Transformando la fracción impropia a número mixto
- Marcamos en la recta numérica números enteros.
- Dividimos cada número entero en 3 partes o segmentos (según indica el denominador).
- Contamos desde 0 hasta 5 los segmentos (según indica el numerador).
- Ubicamos la fracción en el 5º segmento.
- Marcamos en la recta numérica números enteros.
- Dividimos cada número entero en 3 partes o segmentos (según indica el denominador).
- Ubicamos la fracción
en la recta numérica entre los enteros 1 y 2 en el 2º segmento.
- En una fiesta de cumpleaños hay 4 globos amarillos, 2 globos naranja, 1 azul y 5 rojos. ¿Qué fracción representa cada color? Si se pinchan 5, nos quedan 7 globos, ¿qué fracción del total queda sin explotar? Haz un dibujo para representar la situación.

Números mixtos
Conversión de un número mixto a fracción impropia
Conversión de una fracción impropia a un número mixto
Suma y resta de fracciones
- Si las fracciones tienen el mismo denominador, se suman o restan los numeradores y se pone el mismo denominador.
- Si tienen distintos denominadores, primero se reducen a común denominador y luego se procede como en el caso anterior.
Multiplicación de fracciones
Inversa de una fracción
División de fracciones
La fracción como operador


2- Lectura de fracciones


































Comentarios
Publicar un comentario