MATEMÁTICA 10°
SEMANA DEL 03 AL 06 DE NOVIEMBRE
FESTIVO
SEMANA DEL 26 AL 30 DE OCTUBRE
HALLAR LA ECUACIÓN DE LA CIRCUNFERENCIA CONOCIENDO CENTRO Y UN PUNTO DE ELLA
Ecuación de circunferencia, dado su centro y un punto de ella
Ejercicio:
Calcular la ecuación de la circunferencia de centro (1, 1) y que contiene al punto (-2, 3).
Resolución:

Así la ecuación es:


SEMANA DEL 19 AL 23 DE OCTUBRE
DADA LA ECUACIÓN ORDINARIA DE LA CIRCUNFERENCIA CALCULAR SU ECUACIÓN GENERAL
Ejercicio:
Calcular la ecuación de la circunferencia de centro (1, 1) y que contiene al punto (-2, 3).
Resolución:![]()
Así la ecuación es:![]()

Circunferencia
Todos conocen las circunferencias, saben que pueden trazarse con un compás.
Les resultará natural la siguiente definición:
Ahora vamos a deducir partiendo de esta definición, cuál es la expresión de una circunferencia.
Consideremos el siguiente esquema:
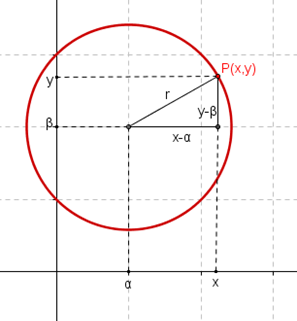
Por teorema de Pitágoras sabemos que los puntos deben cumplir esta ecuación:
Que se llama ecuación ordinaria de la circunferencia con centro y radio .
Si , ¿qué objeto geométrico representa la ecuación?
Todos conocen las circunferencias, saben que pueden trazarse con un compás.
Les resultará natural la siguiente definición:
Ahora vamos a deducir partiendo de esta definición, cuál es la expresión de una circunferencia.
Consideremos el siguiente esquema:

Por teorema de Pitágoras sabemos que los puntos deben cumplir esta ecuación:
Que se llama ecuación ordinaria de la circunferencia con centro y radio .
Si , ¿qué objeto geométrico representa la ecuación?
Desde ecuación ordinaria hacia ecuación general
A partir de la ecuación ordinaria de la circunferencia, desarrollemos los cuadrados de binomio:
Y ahora reagrupemos los términos:
Y renombremos las constantes:
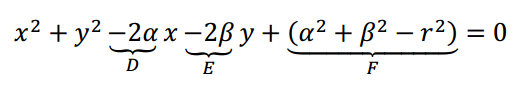
Se obtiene la ecuación:
llamada ecuación general de la circunferencia.
A partir de la ecuación ordinaria de la circunferencia, desarrollemos los cuadrados de binomio:
Y ahora reagrupemos los términos:
Y renombremos las constantes:
![]()
Se obtiene la ecuación:
llamada ecuación general de la circunferencia.
SEMANA DEL 28 de SEPTIEMBRE AL 02 DE OCTUBRE
Circunferencia
Todos conocen las circunferencias, saben que pueden trazarse con un compás.
Les resultará natural la siguiente definición:
Ahora vamos a deducir partiendo de esta definición, cuál es la expresión de una circunferencia.
Consideremos el siguiente esquema:

Por teorema de Pitágoras sabemos que los puntos deben cumplir esta ecuación:
Que se llama ecuación ordinaria de la circunferencia con centro y radio .
Si , ¿qué objeto geométrico representa la ecuación?
Tabla de contenidos [mostrar]
Todos conocen las circunferencias, saben que pueden trazarse con un compás.
Les resultará natural la siguiente definición:
Ahora vamos a deducir partiendo de esta definición, cuál es la expresión de una circunferencia.
Consideremos el siguiente esquema:

Por teorema de Pitágoras sabemos que los puntos deben cumplir esta ecuación:
Que se llama ecuación ordinaria de la circunferencia con centro y radio .
Si , ¿qué objeto geométrico representa la ecuación?
Tabla de contenidos [mostrar]
Ecuación canónica de la circunferencia
Hay un caso particular de circunferencia, que tiene su centro en el origen. La ecuación que la define se llama ecuación canónica de la circunferencia:
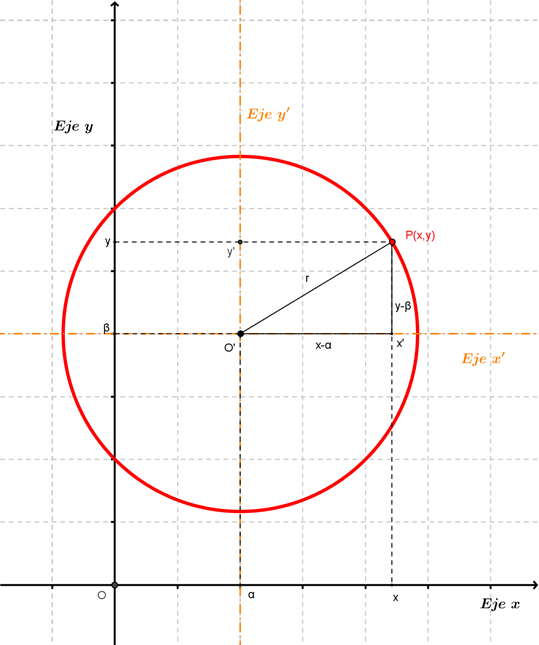
Si la circunferencia no está centrada en el , es posible armar un nuevo sistema de modo tal que el centro de la circunferencia coincida con el nuevo origen de coordenadas. Por ejemplo consideremos:
Si hacemos un cambio de variables:
En las nuevas variables la ecuación queda expresada en forma canónica:
Para obtener la ecuación canónica, hicimos una traslación de ejes, de modo que el centro del nuevo sistema coincidiera con el centro de la circunferencia:
Hay un caso particular de circunferencia, que tiene su centro en el origen. La ecuación que la define se llama ecuación canónica de la circunferencia:
Si la circunferencia no está centrada en el , es posible armar un nuevo sistema de modo tal que el centro de la circunferencia coincida con el nuevo origen de coordenadas. Por ejemplo consideremos:
Si hacemos un cambio de variables:
En las nuevas variables la ecuación queda expresada en forma canónica:
Para obtener la ecuación canónica, hicimos una traslación de ejes, de modo que el centro del nuevo sistema coincidiera con el centro de la circunferencia:

Ejemplo
Encuentre la ecuación de una circunferencia si los extremos de uno de sus diámetros son y .
Conociendo los extremos de un diámetro, ¿cómo obtendrían el centro? ¿Y el radio?
Encuentre la ecuación de una circunferencia si los extremos de uno de sus diámetros son y .
Conociendo los extremos de un diámetro, ¿cómo obtendrían el centro? ¿Y el radio?
Resolución
Como el segmento es un diámetro, el centro es el punto medio de este segmento. Y el radio es la mitad de la distancia entre :
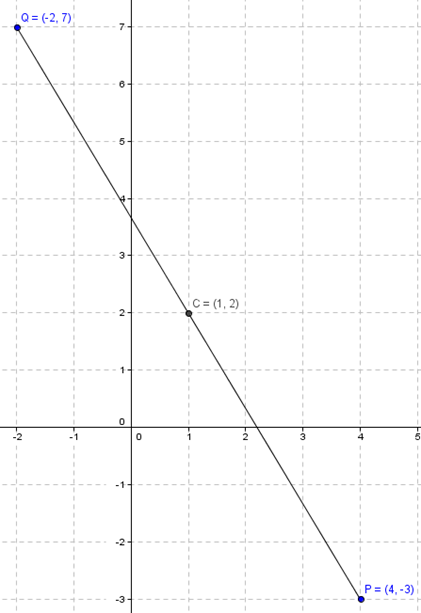
Entonces ya tenemos las coordenadas del centro, y tenemos el radio. Basta con reemplazar en la ecuación ordinaria para obtener la ecuación de esta circunferencia:
La gráfica es:
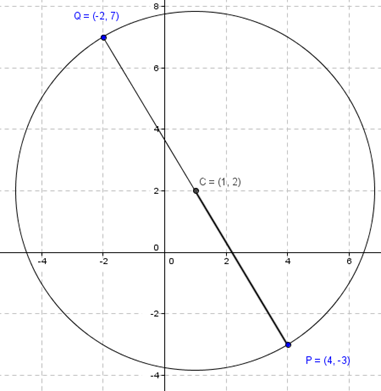
Como el segmento es un diámetro, el centro es el punto medio de este segmento. Y el radio es la mitad de la distancia entre :

Entonces ya tenemos las coordenadas del centro, y tenemos el radio. Basta con reemplazar en la ecuación ordinaria para obtener la ecuación de esta circunferencia:
La gráfica es:

Desde ecuación ordinaria hacia ecuación general
A partir de la ecuación ordinaria de la circunferencia, desarrollemos los cuadrados de binomio:
Y ahora reagrupemos los términos:
Y renombremos las constantes:
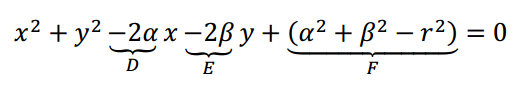
Se obtiene la ecuación:
llamada ecuación general de la circunferencia.
A partir de la ecuación ordinaria de la circunferencia, desarrollemos los cuadrados de binomio:
Y ahora reagrupemos los términos:
Y renombremos las constantes:
![]()
Se obtiene la ecuación:
llamada ecuación general de la circunferencia.
Desde ecuación general a ecuación ordinaria
Hemos obtenido a partir de la ecuación ordinaria, la ecuación general de una circunferencia.
Pero dada una ecuación que tiene este aspecto:
Si se la pasa a la forma de ecuación ordinaria: ¿siempre se obtendrá una circunferencia?
Para responder esto vamos a recordar cómo se completa cuadrados con un ejemplo.
Hemos obtenido a partir de la ecuación ordinaria, la ecuación general de una circunferencia.
Pero dada una ecuación que tiene este aspecto:
Si se la pasa a la forma de ecuación ordinaria: ¿siempre se obtendrá una circunferencia?
Para responder esto vamos a recordar cómo se completa cuadrados con un ejemplo.
Ejemplo
Vamos a completar cuadrados en la siguiente expresión:
La pregunta es: ¿qué lugar geométrico representa esta ecuación? ¿Estamos seguros de que es una circunferencia? Tendremos que llevarla a la forma ordinaria.
La idea es transformar:
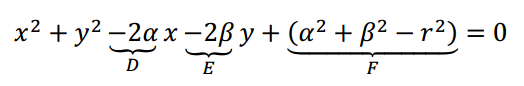
Y además:
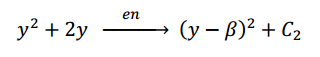
Empecemos con
¿Qué le falta a esta expresión para ser un trinomio cuadrado perfecto? Falta el término independiente. Sabemos que el término independiente deberá ser la mitad de 4, elevado al cuadrado.
Entonces podemos sumar y restar :
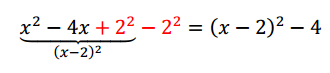
Ahora con la expresión para la variable :
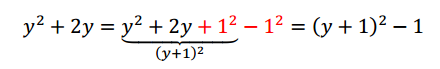
Reemplazamos en la :
Y ahora reordenamos para obtener la ecuación de la circunferencia:
¿Cuáles son el centro y el radio?
Vamos a completar cuadrados en la siguiente expresión:
La pregunta es: ¿qué lugar geométrico representa esta ecuación? ¿Estamos seguros de que es una circunferencia? Tendremos que llevarla a la forma ordinaria.
La idea es transformar:
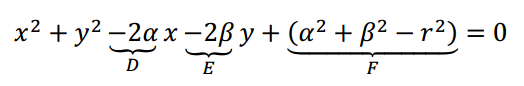
Y además:
![]()
Empecemos con
¿Qué le falta a esta expresión para ser un trinomio cuadrado perfecto? Falta el término independiente. Sabemos que el término independiente deberá ser la mitad de 4, elevado al cuadrado.
Entonces podemos sumar y restar :
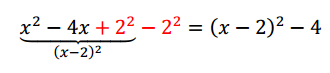
Ahora con la expresión para la variable :
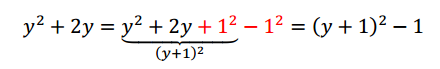
Reemplazamos en la :
Y ahora reordenamos para obtener la ecuación de la circunferencia:
¿Cuáles son el centro y el radio?
Ejercicio para el lector 1
Completando cuadrados, hallen el lugar geométrico correspondiente a cada una de las ecuaciones:
a)
b)
Completando cuadrados, hallen el lugar geométrico correspondiente a cada una de las ecuaciones:
a)
b)
Resumen
De la resolución de los puntos anteriores se desprende la conclusión que presentamos a continuación:

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN
SEMANA DEL 21 AL 25 SEPTIEMBRE
ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN
REPASO
De la resolución de los puntos anteriores se desprende la conclusión que presentamos a continuación:

Ecuación de la circunferencia con centro fuera del origen
La ecuación de la circunferencia con centro en el punto  y radio
y radio  es:
es:
Ejemplo 1
Calcula la ecuación de la circunferencia que tiene su centro en el punto  y radio
y radio  .
.
Ya sabemos que el centro es  y el radio es 4. Solamente debemos sustituir los datos en la fórmula:
y el radio es 4. Solamente debemos sustituir los datos en la fórmula:
Calcula la ecuación de la circunferencia que tiene su centro en el punto ![]() y radio
y radio ![]() .
.

Ejemplo 2
Calcula la ecuación de la circunferencia que tiene su centro en el punto  y es tangente al eje
y es tangente al eje  .
.
En este caso sabemos que la circunferencia es tangente al eje  . Esta información nos ayudará a calcular el radio de la circunferencia. Empezamos dibujando la situación:
. Esta información nos ayudará a calcular el radio de la circunferencia. Empezamos dibujando la situación:
Del dibujo se deduce que el radio de la circunferencia es 2.
Ahora que conocemos dónde está el centro y la medida del radio de la circunferencia, podemos calcular su ecuación:
Observa cómo la figura indica de inmediato la medida del radio. En este caso sencillo, también es posible darse cuenta imaginándose la figura. Pero eso no siempre ocurrirá. En otros problemas te verás obligado a realizar la figura para poder encontrar cómo están relacionados los datos contenidos en el texto del problema.
En algunos casos tendremos que utilizar fórmulas que ya conoces, principalmente las que estudiamos en la primera unidad del curso. El siguiente ejemplo muestra uno de esos casos.
Calcula la ecuación de la circunferencia que tiene su centro en el punto ![]() y es tangente al eje
y es tangente al eje ![]() .
.

Del dibujo se deduce que el radio de la circunferencia es 2.
Ahora que conocemos dónde está el centro y la medida del radio de la circunferencia, podemos calcular su ecuación:
Observa cómo la figura indica de inmediato la medida del radio. En este caso sencillo, también es posible darse cuenta imaginándose la figura. Pero eso no siempre ocurrirá. En otros problemas te verás obligado a realizar la figura para poder encontrar cómo están relacionados los datos contenidos en el texto del problema.
En algunos casos tendremos que utilizar fórmulas que ya conoces, principalmente las que estudiamos en la primera unidad del curso. El siguiente ejemplo muestra uno de esos casos.
Ejemplo 3
Calcula la ecuación de la circunferencia que tiene su centro en el punto  y que pasa por el punto
y que pasa por el punto 
Empezamos dibujando la situación en un sistema de ejes coordenados:
Ahora vemos que el radio de la circunferencia es la distancia desde el centro de la circunferencia  hasta el punto
hasta el punto  .
.
Vamos a calcular esta distancia usando la fórmula de distancia entre dos puntos:
Ahora podemos calcular la ecuación de la circunferencia:
Esta es la ecuación buscada.
SEMANA DEL 07 AL 11 SEPTIEMBRE
ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN
Calcula la ecuación de la circunferencia que tiene su centro en el punto ![]() y que pasa por el punto
y que pasa por el punto ![]()

Ahora vemos que el radio de la circunferencia es la distancia desde el centro de la circunferencia ![]() hasta el punto
hasta el punto ![]() .
.
Vamos a calcular esta distancia usando la fórmula de distancia entre dos puntos:
Ahora podemos calcular la ecuación de la circunferencia:
Esta es la ecuación buscada.
Ecuacion de la circunferencia con centro fuera en el origen
ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO (h,k)
Ecuación de la circunferencia con centro fuera del origen
Ejemplo 1
Ya conoces la ecuación de la circunferencia que tiene su centro en el origen. Si trasladamos el centro de la circunferencia  unidades a la derecha y
unidades a la derecha y  unidades hacia arriba, obtenemos una circunferencia que está fuera del origen. En este caso obtenemos la circunferencia que obtuvimos cuando caracterizamos la circunferencia.
unidades hacia arriba, obtenemos una circunferencia que está fuera del origen. En este caso obtenemos la circunferencia que obtuvimos cuando caracterizamos la circunferencia.
Contenido [Mostrar]
Ya conoces la ecuación de la circunferencia que tiene su centro en el origen. Si trasladamos el centro de la circunferencia ![]() unidades a la derecha y
unidades a la derecha y ![]() unidades hacia arriba, obtenemos una circunferencia que está fuera del origen. En este caso obtenemos la circunferencia que obtuvimos cuando caracterizamos la circunferencia.
unidades hacia arriba, obtenemos una circunferencia que está fuera del origen. En este caso obtenemos la circunferencia que obtuvimos cuando caracterizamos la circunferencia.
Contenido [Mostrar]
Ecuación de la circunferencia con centro fuera del origen
La ecuación de la circunferencia con centro en el punto  y radio
y radio  es:
es:
Ejemplo 1
Calcula la ecuación de la circunferencia que tiene su centro en el punto  y radio
y radio  .
.
Ya sabemos que el centro es  y el radio es 4. Solamente debemos sustituir los datos en la fórmula:
y el radio es 4. Solamente debemos sustituir los datos en la fórmula:
Calcula la ecuación de la circunferencia que tiene su centro en el punto ![]() y radio
y radio ![]() .
.

Ejemplo 2
Calcula la ecuación de la circunferencia que tiene su centro en el punto  y es tangente al eje
y es tangente al eje  .
.
En este caso sabemos que la circunferencia es tangente al eje  . Esta información nos ayudará a calcular el radio de la circunferencia. Empezamos dibujando la situación:
. Esta información nos ayudará a calcular el radio de la circunferencia. Empezamos dibujando la situación:
Del dibujo se deduce que el radio de la circunferencia es 2.
Ahora que conocemos dónde está el centro y la medida del radio de la circunferencia, podemos calcular su ecuación:
Observa cómo la figura indica de inmediato la medida del radio. En este caso sencillo, también es posible darse cuenta imaginándose la figura. Pero eso no siempre ocurrirá. En otros problemas te verás obligado a realizar la figura para poder encontrar cómo están relacionados los datos contenidos en el texto del problema.
En algunos casos tendremos que utilizar fórmulas que ya conoces, principalmente las que estudiamos en la primera unidad del curso. El siguiente ejemplo muestra uno de esos casos.
Calcula la ecuación de la circunferencia que tiene su centro en el punto ![]() y es tangente al eje
y es tangente al eje ![]() .
.

Del dibujo se deduce que el radio de la circunferencia es 2.
Ahora que conocemos dónde está el centro y la medida del radio de la circunferencia, podemos calcular su ecuación:
Observa cómo la figura indica de inmediato la medida del radio. En este caso sencillo, también es posible darse cuenta imaginándose la figura. Pero eso no siempre ocurrirá. En otros problemas te verás obligado a realizar la figura para poder encontrar cómo están relacionados los datos contenidos en el texto del problema.
En algunos casos tendremos que utilizar fórmulas que ya conoces, principalmente las que estudiamos en la primera unidad del curso. El siguiente ejemplo muestra uno de esos casos.
Ejemplo 3
Calcula la ecuación de la circunferencia que tiene su centro en el punto  y que pasa por el punto
y que pasa por el punto 
Empezamos dibujando la situación en un sistema de ejes coordenados:
Ahora vemos que el radio de la circunferencia es la distancia desde el centro de la circunferencia  hasta el punto
hasta el punto  .
.
Vamos a calcular esta distancia usando la fórmula de distancia entre dos puntos:
Ahora podemos calcular la ecuación de la circunferencia:
Esta es la ecuación buscada.
SEMANA DEL 31 DE AGOSTO AL 04 SEPTIEMBRE
LA CIRCUNFERENCIA: ECUACIÓN (0,0) , ECUACIÓN (h,k)
Calcula la ecuación de la circunferencia que tiene su centro en el punto ![]() y que pasa por el punto
y que pasa por el punto ![]()

Ahora vemos que el radio de la circunferencia es la distancia desde el centro de la circunferencia ![]() hasta el punto
hasta el punto ![]() .
.
Vamos a calcular esta distancia usando la fórmula de distancia entre dos puntos:
Ahora podemos calcular la ecuación de la circunferencia:
Esta es la ecuación buscada.
ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN (0,0)
Cuando el centro está en el origen (0, 0), la ecuación de una circunferencia se simplifica a:
A está ecuación se le conoce como ecuación canónica y se da cuando el centro de la circunferencia es el punto C(0,0), por lo que la expresión ordinaria queda reducida a:

Ejemplo: Determinar la ecuación de la circunferencia que pasa por el punto 6,3 y cuyo centro se encuentra en C(0,0)
Nota:La circunferencia con centro en el origen y de radio igual a la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.
Cuando el centro está en el origen (0, 0), la ecuación de una circunferencia se simplifica a: A está ecuación se le conoce como ecuación canónica y se da cuando el centro de la circunferencia es el punto C(0,0), por lo que la expresión ordinaria queda reducida a:  Ejemplo: Determinar la ecuación de la circunferencia que pasa por el punto 6,3 y cuyo centro se encuentra en C(0,0) Nota: La circunferencia con centro en el origen y de radio igual a la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria. |
ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO (h,k)
SEMANA DEL 24 DE AGOSTO AL 29 DE AGOSTO
LAS CÓNICASLA CIRCUNFERENCIA: ECUACIÓN GENENAL, ECUACIÓN CANÓNICA, CENTRO 0,0, CENTRO h,k
Circunferencia
Todos conocen las circunferencias, saben que pueden trazarse con un compás.
Les resultará natural la siguiente definición:
Ahora vamos a deducir partiendo de esta definición, cuál es la expresión de una circunferencia.
Consideremos el siguiente esquema:

Por teorema de Pitágoras sabemos que los puntos deben cumplir esta ecuación:
Que se llama ecuación ordinaria de la circunferencia con centro y radio .
Si , ¿qué objeto geométrico representa la ecuación?
Todos conocen las circunferencias, saben que pueden trazarse con un compás.
Les resultará natural la siguiente definición:
Ahora vamos a deducir partiendo de esta definición, cuál es la expresión de una circunferencia.
Consideremos el siguiente esquema:

Por teorema de Pitágoras sabemos que los puntos deben cumplir esta ecuación:
Que se llama ecuación ordinaria de la circunferencia con centro y radio .
Si , ¿qué objeto geométrico representa la ecuación?
Ecuación canónica de la circunferencia
Hay un caso particular de circunferencia, que tiene su centro en el origen. La ecuación que la define se llama ecuación canónica de la circunferencia:
Si la circunferencia no está centrada en el , es posible armar un nuevo sistema de modo tal que el centro de la circunferencia coincida con el nuevo origen de coordenadas. Por ejemplo consideremos:
Si hacemos un cambio de variables:
En las nuevas variables la ecuación queda expresada en forma canónica:
Para obtener la ecuación canónica, hicimos una traslación de ejes, de modo que el centro del nuevo sistema coincidiera con el centro de la circunferencia:

Hay un caso particular de circunferencia, que tiene su centro en el origen. La ecuación que la define se llama ecuación canónica de la circunferencia:
Si la circunferencia no está centrada en el , es posible armar un nuevo sistema de modo tal que el centro de la circunferencia coincida con el nuevo origen de coordenadas. Por ejemplo consideremos:
Si hacemos un cambio de variables:
En las nuevas variables la ecuación queda expresada en forma canónica:
Para obtener la ecuación canónica, hicimos una traslación de ejes, de modo que el centro del nuevo sistema coincidiera con el centro de la circunferencia:

Ejemplo
Encuentre la ecuación de una circunferencia si los extremos de uno de sus diámetros son y .
Conociendo los extremos de un diámetro, ¿cómo obtendrían el centro? ¿Y el radio?
Encuentre la ecuación de una circunferencia si los extremos de uno de sus diámetros son y .
Conociendo los extremos de un diámetro, ¿cómo obtendrían el centro? ¿Y el radio?
Resolución
Como el segmento es un diámetro, el centro es el punto medio de este segmento. Y el radio es la mitad de la distancia entre :

Entonces ya tenemos las coordenadas del centro, y tenemos el radio. Basta con reemplazar en la ecuación ordinaria para obtener la ecuación de esta circunferencia:
La gráfica es:

Como el segmento es un diámetro, el centro es el punto medio de este segmento. Y el radio es la mitad de la distancia entre :

Entonces ya tenemos las coordenadas del centro, y tenemos el radio. Basta con reemplazar en la ecuación ordinaria para obtener la ecuación de esta circunferencia:
La gráfica es:

Desde ecuación ordinaria hacia ecuación general
A partir de la ecuación ordinaria de la circunferencia, desarrollemos los cuadrados de binomio:
Y ahora reagrupemos los términos:
Y renombremos las constantes:
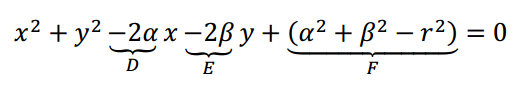
Se obtiene la ecuación:
llamada ecuación general de la circunferencia.
A partir de la ecuación ordinaria de la circunferencia, desarrollemos los cuadrados de binomio:
Y ahora reagrupemos los términos:
Y renombremos las constantes:
![]()
Se obtiene la ecuación:
llamada ecuación general de la circunferencia.
Desde ecuación general a ecuación ordinaria
Hemos obtenido a partir de la ecuación ordinaria, la ecuación general de una circunferencia.
Pero dada una ecuación que tiene este aspecto:
Si se la pasa a la forma de ecuación ordinaria: ¿siempre se obtendrá una circunferencia?
Para responder esto vamos a recordar cómo se completa cuadrados con un ejemplo.
Hemos obtenido a partir de la ecuación ordinaria, la ecuación general de una circunferencia.
Pero dada una ecuación que tiene este aspecto:
Si se la pasa a la forma de ecuación ordinaria: ¿siempre se obtendrá una circunferencia?
Para responder esto vamos a recordar cómo se completa cuadrados con un ejemplo.
Ejemplo
Vamos a completar cuadrados en la siguiente expresión:
La pregunta es: ¿qué lugar geométrico representa esta ecuación? ¿Estamos seguros de que es una circunferencia? Tendremos que llevarla a la forma ordinaria.
La idea es transformar:
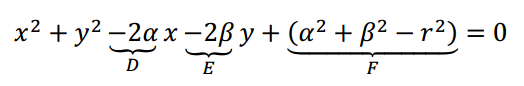
Y además:
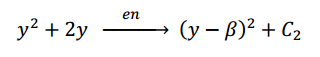
Empecemos con
¿Qué le falta a esta expresión para ser un trinomio cuadrado perfecto? Falta el término independiente. Sabemos que el término independiente deberá ser la mitad de 4, elevado al cuadrado.
Entonces podemos sumar y restar :
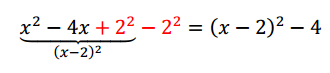
Ahora con la expresión para la variable :
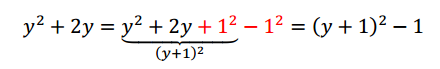
Reemplazamos en la :
Y ahora reordenamos para obtener la ecuación de la circunferencia:
¿Cuáles son el centro y el radio?
SEMANA DEL 17 DE AGOSTO AL 21 DE AGOSTO
NO HUBO ACTIVIDAD-FESTIVO
SEMANA DEL 10 DE AGOSTO AL 14 DE AGOSTO
LEY DEL SENO-CASO II
SEMANA DEL 3 DE AGOSTO AL 07 DE AGOSTO
LEY DEL SENO
SEMANA DEL 27 DE JULIO AL 31 DE JULIO
ÁNGULO DE UN OBJETO CUANDO LA VISUAL ES HACIA ABAJO
ÁNGULO DE DEPRESIÓN: ángulo que se forma entre la línea visual y la horizontal cuando el objeto está por debajo de la horizontal.
SEMANA DEL 13 DE JULIO AL 17 DE JULIO
ÁNGULO DE DEPRESIÓN
ÁNGULO DE DEPRESIÓN: ángulo que se forma entre la línea visual y la horizontal cuando el objeto está por debajo de la horizontal.
EJEMPLOS
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
2. Desde un edificio de 60 m un niño ve un heladero con unángulo de depresión de 37º. Calcular la distancia del heladero a la base del edificio.
3. Sobre un edificio de 30 m un obrero ve la acera de enfrente con un ángulo de depresión de 39º
4. Se observa un automóvil desde la azotea de un edificio de 45 m de altura con un ángulo de depresión de 20º. ¿cuál es la distancia del automóvil a la base del edificio?
5. El ángulo de depresión de la terraza de un edificio es 22º con respecto a un punto situado a 50 m. calcular la altura del edificio.
SEMANA DEL 30 DE JUNIO AL 03 DE JULIO
ÁNGULO DE DEPRESIÓN
ÁNGULO DE DEPRESIÓN: ángulo que se forma entre la línea visual y la horizontal cuando el objeto está por debajo de la horizontal.
EJEMPLOS
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
2. Desde un edificio de 60 m un niño ve un heladero con unángulo de depresión de 37º. Calcular la distancia del heladero a la base del edificio.
3. Sobre un edificio de 30 m un obrero ve la acera de enfrente con un ángulo de depresión de 39º
4. Se observa un automóvil desde la azotea de un edificio de 45 m de altura con un ángulo de depresión de 20º. ¿cuál es la distancia del automóvil a la base del edificio?
5. El ángulo de depresión de la terraza de un edificio es 22º con respecto a un punto situado a 50 m. calcular la altura del edificio.
SEMANA 22 AL 26 DE JUNIO
ÁNGULO DE DEPRESIÓN
ÁNGULO DE DEPRESIÓN: ángulo que se forma entre la línea visual y la horizontal cuando el objeto está por debajo de la horizontal.
EJEMPLOS
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
2. Desde un edificio de 60 m un niño ve un heladero con unángulo de depresión de 37º. Calcular la distancia del heladero a la base del edificio.
3. Sobre un edificio de 30 m un obrero ve la acera de enfrente con un ángulo de depresión de 39º
4. Se observa un automóvil desde la azotea de un edificio de 45 m de altura con un ángulo de depresión de 20º. ¿cuál es la distancia del automóvil a la base del edificio?
5. El ángulo de depresión de la terraza de un edificio es 22º con respecto a un punto situado a 50 m. calcular la altura del edificio.
Vamos a completar cuadrados en la siguiente expresión:
La pregunta es: ¿qué lugar geométrico representa esta ecuación? ¿Estamos seguros de que es una circunferencia? Tendremos que llevarla a la forma ordinaria.
La idea es transformar:
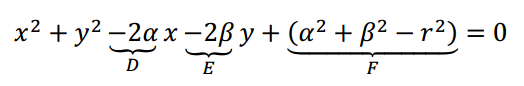
Y además:
![]()
Empecemos con
¿Qué le falta a esta expresión para ser un trinomio cuadrado perfecto? Falta el término independiente. Sabemos que el término independiente deberá ser la mitad de 4, elevado al cuadrado.
Entonces podemos sumar y restar :
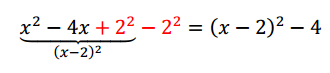
Ahora con la expresión para la variable :
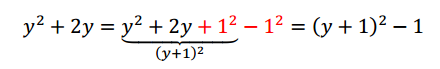
Reemplazamos en la :
Y ahora reordenamos para obtener la ecuación de la circunferencia:
¿Cuáles son el centro y el radio?
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
SEMANA 15 AL 19 DE JUNIO
ÁNGULO DE DEPRESIÓN
ÁNGULO DE DEPRESIÓN: ángulo que se forma entre la línea visual y la horizontal cuando el objeto está por debajo de la horizontal.
EJEMPLOS
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
2. Desde un edificio de 60 m un niño ve un heladero con unángulo de depresión de 37º. Calcular la distancia del heladero a la base del edificio.
3. Sobre un edificio de 30 m un obrero ve la acera de enfrente con un ángulo de depresión de 39º
4. Se observa un automóvil desde la azotea de un edificio de 45 m de altura con un ángulo de depresión de 20º. ¿cuál es la distancia del automóvil a la base del edificio?
5. El ángulo de depresión de la terraza de un edificio es 22º con respecto a un punto situado a 50 m. calcular la altura del edificio.
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
SEMANA 08 AL 12 DE JUNIO
ÁNGULO DE DEPRESIÓN
ÁNGULO DE DEPRESIÓN: ángulo que se forma entre la línea visual y la horizontal cuando el objeto está por debajo de la horizontal.
EJEMPLOS
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
2. Desde un edificio de 60 m un niño ve un heladero con unángulo de depresión de 37º. Calcular la distancia del heladero a la base del edificio.
3. Sobre un edificio de 30 m un obrero ve la acera de enfrente con un ángulo de depresión de 39º
4. Se observa un automóvil desde la azotea de un edificio de 45 m de altura con un ángulo de depresión de 20º. ¿cuál es la distancia del automóvil a la base del edificio?
5. El ángulo de depresión de la terraza de un edificio es 22º con respecto a un punto situado a 50 m. calcular la altura del edificio.
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
SEMANA 01 AL 05 DE JUNIO
ÁNGULO DE DEPRESIÓN
ÁNGULO DE DEPRESIÓN: ángulo que se forma entre la línea visual y la horizontal cuando el objeto está por debajo de la horizontal.
EJEMPLOS
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
2. Desde un edificio de 60 m un niño ve un heladero con unángulo de depresión de 37º. Calcular la distancia del heladero a la base del edificio.
3. Sobre un edificio de 30 m un obrero ve la acera de enfrente con un ángulo de depresión de 39º
4. Se observa un automóvil desde la azotea de un edificio de 45 m de altura con un ángulo de depresión de 20º. ¿cuál es la distancia del automóvil a la base del edificio?
5. El ángulo de depresión de la terraza de un edificio es 22º con respecto a un punto situado a 50 m. calcular la altura del edificio.
SEMANA 01 AL 05 DE JUNIO
- Un avión militar ve un objetivo a bombardear con un ángulo de depresión de 30º, si el objetivo dista 15 m del avión, calcular la altura del avión.
SEMANA 25 AL 29 DE MAYO
SEMANA 25 AL 29 DE MAYO
SEMANA 18 AL 22 DE MAYO
SEMANA 18 AL 22 DE MAYO
SEMANA 11 AL 15 DE MAYO
SEMANA 11 AL 15 DE MAYO
SEMANA 4 AL 8 DE MAYO
CÁLCULO DE FUNCIONES TRIGONOMÉTRICAS
EN UN TRIÁNGULO RECTÁNGULO
SEMANA 4 AL 8 DE MAYO
Triángulos rectángulos: ¿Qué elementos tienen? ¿Cómo se relacionan los elementos de un triángulo rectángulo?
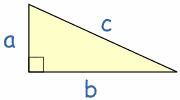
Los triángulos en general, están formados por 3 lados y 3 ángulos. Además, los triángulos rectángulos se llaman así por tener un ángulo recto entre sus catetos.
Los lados de un triángulo rectángulo son la hipotenusa y los dos catetos:
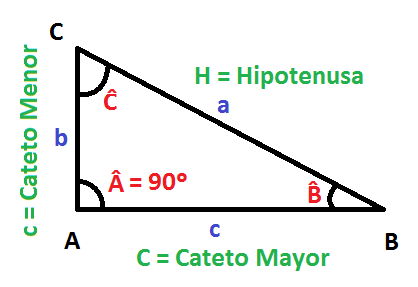 El lado que está enfrente del ángulo recto es la hipotenusa:
El lado que está enfrente del ángulo recto es la hipotenusa:
 A los otros dos lados, son los catetos: cateto mayor y cateto menor, que como su propio nombre indican, el cateto mayor es el que tiene una mayor longitud y el cateto menor es el que tiene una menor longitud.
Pero existe otra forma de denominar a los catetos, en función del ángulo que tomemos de referencia: el cateto opuesto y contiguo (o cateto adyacente).
A los otros dos lados, son los catetos: cateto mayor y cateto menor, que como su propio nombre indican, el cateto mayor es el que tiene una mayor longitud y el cateto menor es el que tiene una menor longitud.
Pero existe otra forma de denominar a los catetos, en función del ángulo que tomemos de referencia: el cateto opuesto y contiguo (o cateto adyacente).

¿Cómo identificar los catetos en un triángulo rectángulo?
Te voy a explicar cómo diferenciar entre el cateto opuesto y el cateto contiguo en función del ángulo de referencia.
¿Cómo saber cuál es el cateto opuesto?
Se le llama cateto opuesto al lado que esté enfrente del ángulo de referencia
¿Cómo saber cuál es el cateto contiguo o cateto adyacente?
Se le llama cateto contiguo al lado que esté tocando a ese ángulo.
Por ejemplo, en este triángulo:
 Si tomamos de referencia el ángulo B:
Si tomamos de referencia el ángulo B:
 b es el lado que está enfrente de B y c es el lado que está tocando al ángulo B.
Pero si tomamos como referencia al ángulo C:
b es el lado que está enfrente de B y c es el lado que está tocando al ángulo B.
Pero si tomamos como referencia al ángulo C:
 Entonces b es el cateto contiguo y c es el cateto opuesto.
Por tanto, para saber cuál de todas las razones trigonométricas en el triángulo rectángulo, tienes que utilizar para resolver un problema, lo primero que tienes que hacer es identificar tus catetos con respecto al ángulo con el que estés calculándolas.
Los lados y ángulos del triángulo rectángulo, tienen una serie de relaciones entre ellos, las cuales nos van a ayudar a calcular las medidas de los elementos que no conozcamos.
Entonces b es el cateto contiguo y c es el cateto opuesto.
Por tanto, para saber cuál de todas las razones trigonométricas en el triángulo rectángulo, tienes que utilizar para resolver un problema, lo primero que tienes que hacer es identificar tus catetos con respecto al ángulo con el que estés calculándolas.
Los lados y ángulos del triángulo rectángulo, tienen una serie de relaciones entre ellos, las cuales nos van a ayudar a calcular las medidas de los elementos que no conozcamos.
- Los tres lados están relacionados por el teorema de Pitágoras:

- Los tres ángulos suman entre ellos 180º:

- Los lados y los ángulos se relacionan mediante las razones trigonométricas, las cuales te las explico con todo detalle en el siguiente apartado.



Razones trigonométricas de un triángulo rectángulo
Los ángulos y lados de un triángulo rectángulo, están relacionados por unas expresiones a las que llamamos razones trigonométricas.
Vamos ir viéndolas una por una, tomando como ángulo de referencia el ángulo B.
Seno del ángulo B
Relaciona el ángulo B con el cateto opuesto y la hipotenusa. En otras palabras, es la razón entre el cateto opuesto y la hipotenusa. Se expresa como sen B:
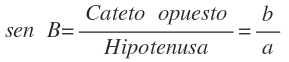
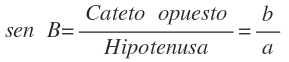
Coseno del ángulo B
Relaciona el ángulo B con el cateto contiguo y la hipotenusa. Es la razón entre el cateto contiguo y la hipotenusa. Se expresa como cos B:
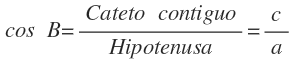
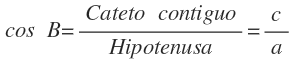
Tangente del ángulo B
Es la razón entre el cateto opuesto y el cateto contiguo. También entre el seno y el coseno. Se expresa como tg B:


Cosecante del ángulo B
Es la razón inversa del seno. Se expresa como cosec B:
 No hay que confundirlo con la función inversa del seno, que es el arco seno.
No hay que confundirlo con la función inversa del seno, que es el arco seno.

Secante del ángulo B
Es la razón inversa del coseno. Se expresa como sec B:
 No hay que confundirlo con la función inversa del coseno que es el arco coseno.
No hay que confundirlo con la función inversa del coseno que es el arco coseno.

Cotangente del ángulo B
Es la razón inversa de la tangente y se expresa como cotg B:
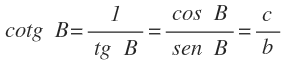 No hay que confundirlo por la función inversa de la tangente que es el arco tangente.
Como ves, todas la razones trigonométricas relacionan un ángulo con dos lados, es decir, tres variables. Por tanto, a la hora de elegir que razón utilizar, deberá ser aquella que sepamos al menos dos de las tres variables.
Tenemos que ir jugando con estas fórmulas según los datos que nos de el enunciado del problema.
Existen dos casos posibles que podemos encontrarnos en los problemas o ejercicios de resolución de triángulos rectángulos que son:
No hay que confundirlo por la función inversa de la tangente que es el arco tangente.
Como ves, todas la razones trigonométricas relacionan un ángulo con dos lados, es decir, tres variables. Por tanto, a la hora de elegir que razón utilizar, deberá ser aquella que sepamos al menos dos de las tres variables.
Tenemos que ir jugando con estas fórmulas según los datos que nos de el enunciado del problema.
Existen dos casos posibles que podemos encontrarnos en los problemas o ejercicios de resolución de triángulos rectángulos que son:
- Que conozcamos dos lados y nos pregunte por algún ángulo o el otro lado
- Que conozcamos un lado y un ángulo y nos pidan calcular cualquier otro lado o ángulo
Si nos dan como dato dos ángulos, no podremos calcular los lados de ese triángulo rectángulo. Necesitaríamos más información.
Siempre necesitamos como mínimo dos datos para calcular un tercero.
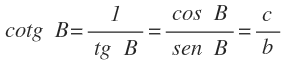
Resolución de triángulos rectángulos cuando se conocen dos lados
Vamos a ver, todo lo que te acabo de explicar con un ejemplo. Tenemos un triángulo del que conocemos 2 de sus lados:
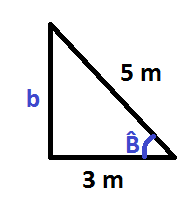 Nos piden calcular el lado b y el ángulo B:
Para calcular el lado b, lo hacemos mediante la fórmula de Pitágoras, ya que en esa fórmula se relacionan los 3 lados y sólo nos queda por conocer 1 un lado.
De la fórmula de Pitágoras despejamos el cateto mayor, que corresponde con el lado b:
Nos piden calcular el lado b y el ángulo B:
Para calcular el lado b, lo hacemos mediante la fórmula de Pitágoras, ya que en esa fórmula se relacionan los 3 lados y sólo nos queda por conocer 1 un lado.
De la fórmula de Pitágoras despejamos el cateto mayor, que corresponde con el lado b:
 Y ahora sustituimos valores y calculamos:
Y ahora sustituimos valores y calculamos:
- C = b (es el lado que estamos calculando)
- c = 3 m
- H = 5 m
 Nos ha quedado una ecuación, de la que tenemos b como incógnita.
Para calcular el ángulo B, podemos hacerlo de muchas maneras. Una de ellas es utilizando la razón trigonométrica del seno por ejemplo, ya que conocemos el valor de la hipotenusa y del cateto opuesto.
En realidad podríamos utilizar cualquier razón trigonométrica porque conocemos todos sus lados:
Nos ha quedado una ecuación, de la que tenemos b como incógnita.
Para calcular el ángulo B, podemos hacerlo de muchas maneras. Una de ellas es utilizando la razón trigonométrica del seno por ejemplo, ya que conocemos el valor de la hipotenusa y del cateto opuesto.
En realidad podríamos utilizar cualquier razón trigonométrica porque conocemos todos sus lados:
 Sustituimos valores y resolvemos:
Sustituimos valores y resolvemos:
 Una vez conocemos el valor del seno de B, con la calculadora hemos calculado su inversa y obtenemos el ángulo. Presta atención a que la calculadora esté en grados y no en radianes.
Una vez conocemos el valor del seno de B, con la calculadora hemos calculado su inversa y obtenemos el ángulo. Presta atención a que la calculadora esté en grados y no en radianes.





Resolución de triángulos rectángulos cuando se conocen un lado y un ángulo
Vamos a ver otro ejemplo con este triángulo, del que conocemos un ángulo y un lado.
 Nos piden calcular el lado c:
A priori, no se puede utilizar la fórmula de Pitágoras porque sólo tengo el dato de un lado. Por tanto, queda utilizar las razones trigonométricas.
Conocemos la hipotenusa y nos están pidiendo el lado adyacente. La razón que relaciona éstos dos lados es la del coseno:
Nos piden calcular el lado c:
A priori, no se puede utilizar la fórmula de Pitágoras porque sólo tengo el dato de un lado. Por tanto, queda utilizar las razones trigonométricas.
Conocemos la hipotenusa y nos están pidiendo el lado adyacente. La razón que relaciona éstos dos lados es la del coseno: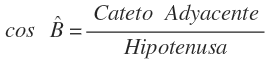 Sustituimos los valores que conocemos y resolvemos:
Sustituimos los valores que conocemos y resolvemos:
- Ángulo B = 60º
- Cateto Adyacente = c
- Hipotenusa = 6 m
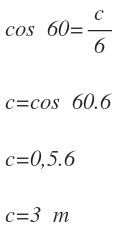 En este caso, el c0seno de 60, una vez resuelto con la calculadora, lo tratamos como un número más.
Ahora que ya conocemos c, podríamos utilizar Pitágoras para calcular el lado que nos queda, si nos lo estuvieran pidiendo.
Conforme vamos conociendo más elementos, tenemos la posibilidad de aplicar más relaciones para encontrar la solución que nos pidan.
La resolución de triángulos rectángulos tienen muchas aplicaciones, como calcular la distancia de un cable, calcular la altura de una torre, calcular la distancia de un árbol según su sombra, calcular el ángulo que forma una escalera apoyada en una pared o cualquier otra cosa que nos pueda pedir el enunciado de un problema.
En este caso, el c0seno de 60, una vez resuelto con la calculadora, lo tratamos como un número más.
Ahora que ya conocemos c, podríamos utilizar Pitágoras para calcular el lado que nos queda, si nos lo estuvieran pidiendo.
Conforme vamos conociendo más elementos, tenemos la posibilidad de aplicar más relaciones para encontrar la solución que nos pidan.
La resolución de triángulos rectángulos tienen muchas aplicaciones, como calcular la distancia de un cable, calcular la altura de una torre, calcular la distancia de un árbol según su sombra, calcular el ángulo que forma una escalera apoyada en una pared o cualquier otra cosa que nos pueda pedir el enunciado de un problema.

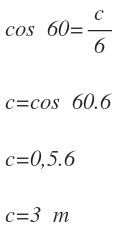
Ejercicio resuelto de resolución de triángulos rectángulos
En el siguiente ejercicio, aplicaremos lo aprendido para calcular diferentes ángulos y lados de un triángulo, que en principio no es rectángulo.
Calcular los lados y los ángulos del siguiente triángulo, del que nos dan uno de los ángulos, uno de los lados y la distancia desde el punto A hasta el punto D:
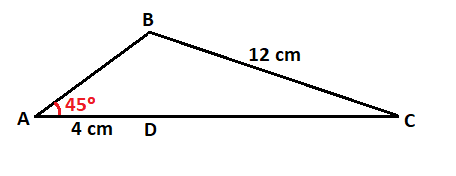 Lo primero que tienes que hacer es buscar triángulos rectángulos en este triángulo para poder resolverlo y calcular los elementos que faltan.
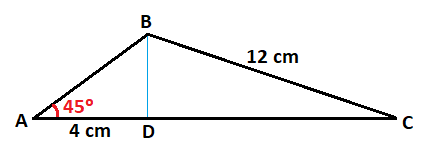
Para ello, trazamos una línea vertical que una al vértice B con el punto D, que es la altura del triángulo y lo divide en dos triángulos rectángulos:
Lo primero que tienes que hacer es buscar triángulos rectángulos en este triángulo para poder resolverlo y calcular los elementos que faltan.
Para ello, trazamos una línea vertical que una al vértice B con el punto D, que es la altura del triángulo y lo divide en dos triángulos rectángulos:
 Empezamos quedándonos con el triángulo de la izquierda:
Empezamos quedándonos con el triángulo de la izquierda:
 En este triángulo falta por calcular el lado c y el lado h (les he llamado c y h por llamarles de alguna forma para distinguirlos).
Vamos a calcular el lado c. Conocemos el ángulo y el lado contiguo al ángulo, pero no conocemos el lado opuesto.
La razón que relaciona esas tres variables es la tangente:
En este triángulo falta por calcular el lado c y el lado h (les he llamado c y h por llamarles de alguna forma para distinguirlos).
Vamos a calcular el lado c. Conocemos el ángulo y el lado contiguo al ángulo, pero no conocemos el lado opuesto.
La razón que relaciona esas tres variables es la tangente:
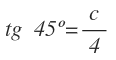 De donde despejamos c:
De donde despejamos c:
 La tangente de 45º la calculamos con la calculadora y finalmente operamos:
La tangente de 45º la calculamos con la calculadora y finalmente operamos:
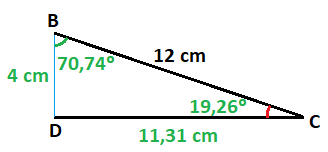
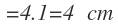 El lado c mide 4 cm.
Ahora calcularemos el lado h, mediante la razón del seno, ya que conocemos el ángulo, el cateto opuesto y no conocemos la hipotenusa:
El lado c mide 4 cm.
Ahora calcularemos el lado h, mediante la razón del seno, ya que conocemos el ángulo, el cateto opuesto y no conocemos la hipotenusa:
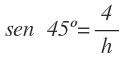 Despejamos h:
Despejamos h:
 Calculamos el seno de 45º con la calculadora y operamos:
Calculamos el seno de 45º con la calculadora y operamos:
 El lado h mide 5,65 cm.
Otra forma de calcular h hubiera sido por el teorema de Pitágoras.
Finalmente vamos a calcular el ángulo que nos falta. Como sabemos que los lados de un triángulo deben sumar 180º, a 180º le restamos los dos ángulos que ya sabemos:
El lado h mide 5,65 cm.
Otra forma de calcular h hubiera sido por el teorema de Pitágoras.
Finalmente vamos a calcular el ángulo que nos falta. Como sabemos que los lados de un triángulo deben sumar 180º, a 180º le restamos los dos ángulos que ya sabemos:
 Por lo que el ángulo que falta mide 45º.
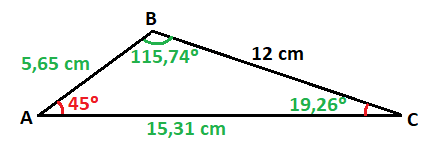
Colocamos todos los datos calculados en el triángulo rectángulo:
Por lo que el ángulo que falta mide 45º.
Colocamos todos los datos calculados en el triángulo rectángulo:
 Hacemos lo mismo con el triángulo rectángulo que nos quedó a la derecha, donde colocamos el valor de uno de los lados que hemos calculado gracias al otro triángulo rectángulo:
Hacemos lo mismo con el triángulo rectángulo que nos quedó a la derecha, donde colocamos el valor de uno de los lados que hemos calculado gracias al otro triángulo rectángulo:
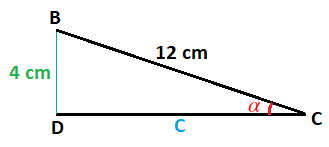 De este triángulo faltaría por calcular el lado C y los dos ángulos que no son rectos.
Empezamos calculando el ángulo alfa. Lo haré mediante la razón del seno, que relaciona el cateto opuesto con la hipotenusa y tengo los dos datos:
De este triángulo faltaría por calcular el lado C y los dos ángulos que no son rectos.
Empezamos calculando el ángulo alfa. Lo haré mediante la razón del seno, que relaciona el cateto opuesto con la hipotenusa y tengo los dos datos:
 Calculo el seno de alfa:
Calculo el seno de alfa:
 Y mediante la inversa del seno, calculo el ángulo:
Y mediante la inversa del seno, calculo el ángulo:
 El ángulo alfa mide 19,26º.
El lado C lo voy a calcular por Pitágoras esta vez:
El ángulo alfa mide 19,26º.
El lado C lo voy a calcular por Pitágoras esta vez:
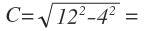
 El lado C mide 11,31 cm.
El ángulo que nos falta lo calcularemos sabiendo que los tres ángulos de un triángulo suman 180º y a 180º le restaré los dos ángulos que ya sabemos:
El lado C mide 11,31 cm.
El ángulo que nos falta lo calcularemos sabiendo que los tres ángulos de un triángulo suman 180º y a 180º le restaré los dos ángulos que ya sabemos:
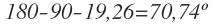 Coloco todos los datos en el triángulo
Coloco todos los datos en el triángulo
 Ahora ya tengo todos los datos que necesito para calcular los lados y los ángulos del triángulo original
Ahora ya tengo todos los datos que necesito para calcular los lados y los ángulos del triángulo original
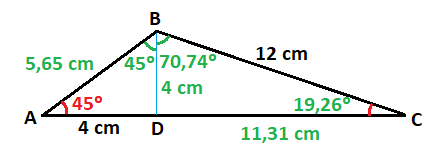 Para calcular el ángulo B, sumo los dos ángulos que he obtenido anteriormente:
Para calcular el ángulo B, sumo los dos ángulos que he obtenido anteriormente:
 Y para calcular el lado inferior, sumo el dato que ya tenía desde el punto A al punto D y el que he calculado desde el punto D al punto C:
Y para calcular el lado inferior, sumo el dato que ya tenía desde el punto A al punto D y el que he calculado desde el punto D al punto C:
 Por lo que los lados y ángulos del triángulo original son:
Por lo que los lados y ángulos del triángulo original son:



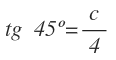
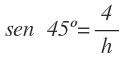







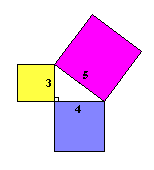
Teorema de Pitágoras
Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos:
... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!
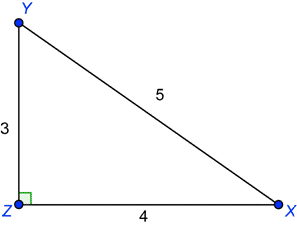
El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)
¿Seguro... ?
Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar.
¿Por qué es útil esto?
Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que sólo funciona en triángulos rectángulos!)
¿Cómo lo uso?
Escríbelo como una ecuación:
Los Lados de un Triángulo Rectángulo
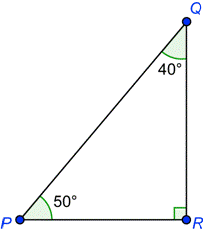
En el ejemplo anterior, uno de los ángulos agudos mide 20°. Podrías describir el lado cuya medida es 4 pies como la altura del triángulo, o podrías decir que es el “opuesto” del ángulo de 20°. El otro lado del triángulo se llama “adyacente” al ángulo de 20°. En trigonometría, este tipo de relación entre lados y ángulos es muy importante. Estos dos lados de un triángulo rectángulo se llaman “catetos”, por lo que el lado opuesto se llama cateto opuesto y el lado adyacente se llama cateto adyacente.
La relación general entre lados y ángulos se muestra en el diagrama siguiente.
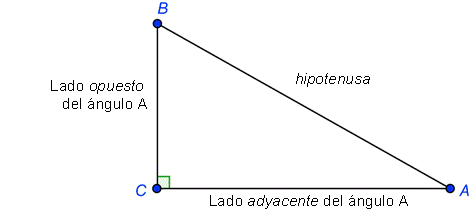
El ángulo A está formado por la hipotenusa y el cateto
Ten en cuenta que las palabras “opuesto” y “adyacente” dependen de qué ángulo se está tratando. El lado opuesto al ángulo no necesariamente es la altura del triángulo. Considera el siguiente ejemplo:
Cada cateto en un triángulo rectángulo es adyacente a uno de los ángulos agudos y opuesto al otro ángulo agudo.
A CONTINUACIÓN SE PRESENTA LA RESPECTIVA VIDEO CLASE:
UNA VEZ VISTO EL VIDEO DESARROLLAR LA SIGUIENTE ACTIVIDAD:
| ||||||||||||||||||||||||||||||||||||||||||||













































Comentarios
Publicar un comentario